专题六圆——2025届中考数学二轮专题达标训练（含解析）

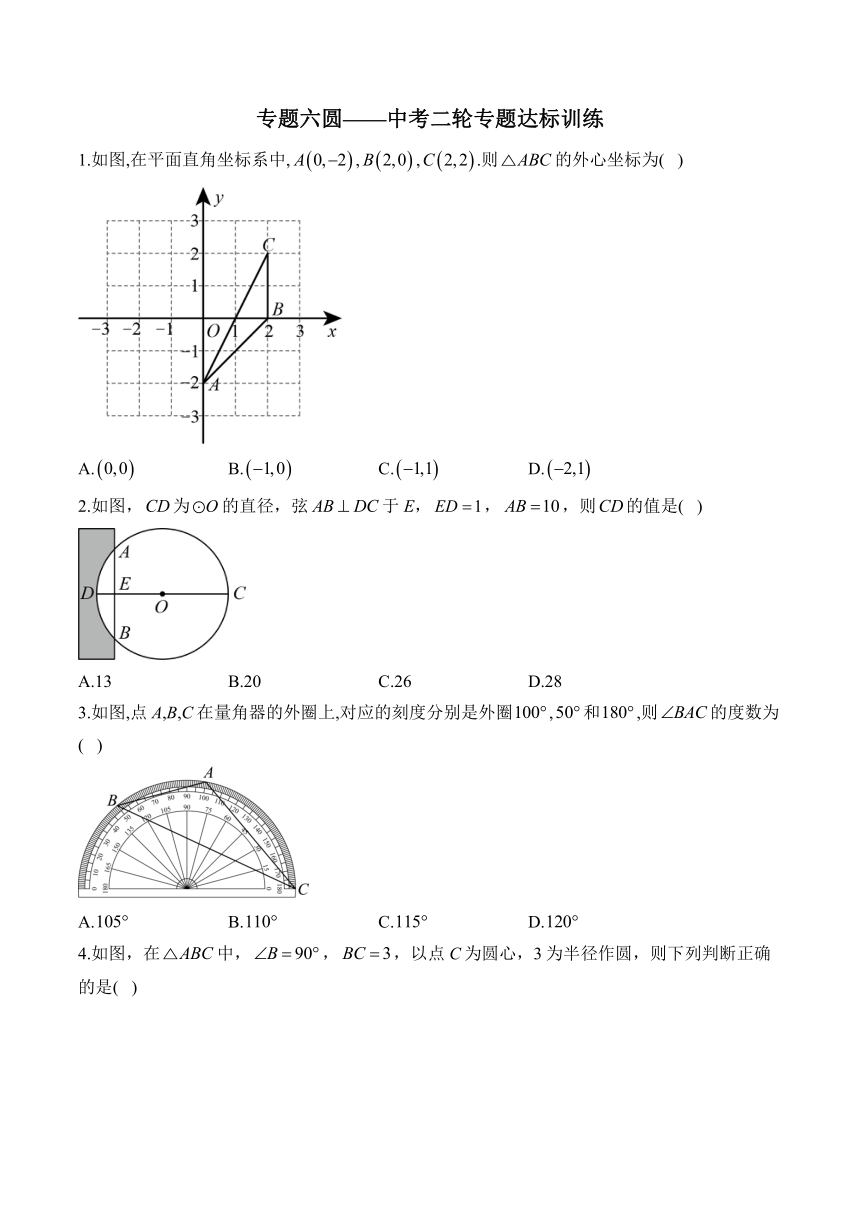
专题六圆———中考二轮专题达标训练 1.如图,在平面直角坐标系中,,,.则的外心坐标为( ) A. B. C. D. 2.如图，为的直径，弦于E，，，则的值是( ) A.13 B.20 C.26 D.28 3.如图,点A,B,C在量角器的外圈上,对应的刻度分别是外圈,和,则的度数为( ) A. B. C. D. 4.如图，在中，，，以点C为圆心，3为半径作圆，则下列判断正确的是( ) A.点B在内 B.点A在上 C.边与相切 D.边与相离 5.如图，四边形内接于，连接，，若，，则的度数是( ) A. B. C. D. 6.如图,、是的两条直径,A是劣弧的中点,若,则的度数是( ) A. B. C. D. 7.如图,正八边形内接于,的半径为2,连接,,则( ) A. B. C. D.2 8.如图,是的直径,点C在上,,垂足为D,,点E是上的动点(不与C重合),点F为的中点,若在E运动过程中的最大值为4,则的值为( ) A. B. C. D. 9.如图,在一张纸片中,,,,O是它的内切圆.小明用剪刀沿着的切线剪下一块三角形,则的周长为( ) A.5 B.6 C.7 D.8 10.如图,点A,B,C在上,,延长交于点D,,,则的长是( ) A. B. C. D. 11.若一个圆锥的母线长为5cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径为_____cm. 12.如图,四边形是的内接四边形,,则_____°. 13.如图，等边是的内接三角形，若的半径为2，则的边长为_____. 14.如图,C,D是以为直径的半圆周的三等分点,.则阴影部分的面积等于_____. 15.如图，点A是半圆上的一个三等分点，点B是的中点，P是直径上一动点，的半径是2，则的最小值为_____. 16.如图,在中,半径,,. (1)求扇形的面积. (2)求的度数. 17.如图,AB是的直径,四边形ABCD内接于,交AC于点E,. (1)求证：； (2)若,,求BC的长. 18.如图,在中,以边为直径作,交边于点D,延长交于点E,连接交于点F,且. (1)求证：； (2)若,求图中阴影部分的面积. 19.如图,是的直径,平分,,垂足为E. (1)求证：是的切线； (2)若,,求的半径. 20.已知，如图，AB是的直径，点C为上一点，于点F，交于点E，AE与BC交于点H，点D为OE的延长线上一点，且. (1)求证：BD是的切线； (2)若的半径为5，，求BH的长. 答案以及解析 1.答案：C 解析：如图,分别作、的垂直平分线交于点P,点即为所求, 故选：C. 2.答案：C 解析：如图，连接， 设圆的半径为x，则， 由垂径定理可得，， 中，， ， 解得：， ， 故选：C. 3.答案：C 解析：如图,点O为外圈所对的圆心,连接、、, 由题意得,, 由圆周角定理可知,,, ∴, 故选：C. 4.答案：C 解析：， 点B在上，A错误，故不符合要求； ， 点A在外，B错误，故不符合要求； ，， 边与相切，C正确，故符合要求； 由题意知，边与相交，D错误，故不符合要求； 故选：C. 5.答案：B 解析：∵四边形内接于， ∴， ∴， ∵，经过圆心， ∴， ∴， ∴， 故选：B. 6.答案：C 解析：如下图,连接, ∵A是劣弧的中点,即, ∴, ∵, ∴, ∵, ∴, 即. 故选：C. 7.答案：A 解析：连接,过点A作于点M, 在正八边形中,, ∵, ∴, ∴, ∴. 在中,, ∴, ∴(负值舍去), ∴. 故选A. 8.答案：A 解析：如图, 连接,, 点F是的中点, , , , , , 点O,D,C,F在以为直径的圆上, , ∵, 在中,,, 根据勾股定理得, 故选A. 9.答案：B 解析：如图,设与相切于点M,切设的内切圆切三边于点F、H、G,连接、、,则,,设的半径为r, ∴, ∴四边形是正方形, ∴, ∵是的切线, ∴, ∵,,, ∴ 由切线长定理可知,,, ∴, ∴, ∴, ∴, ∴的周长. 故选：B. 10.答案：D 解析：如图,连接,,作于点M, ∵, ∴,, ∴,, ∵,, ∴, ∴, ∴, ∵,, ∴, ∴, ∴, ∵, ∴, ∴,, ∵, ∴,, ∴, 故选：D. 11.答案： 解析：设圆锥底面半径为rcm, 则圆锥底面周长为：, ∴侧面展开图的弧长为：, ∴, 解得：, 故答案为：. 12.答案： 解析：∵四边形是的内接四边形,, ∴,, ∴, ∴； 故答案为：130. 13.答案： 解析：是的内接正三角形； ， 过O作于D，连接，则长为边心距 ... ...