5.3正方形培优练习 浙教版2024—2025学年八年级下册（含答案）

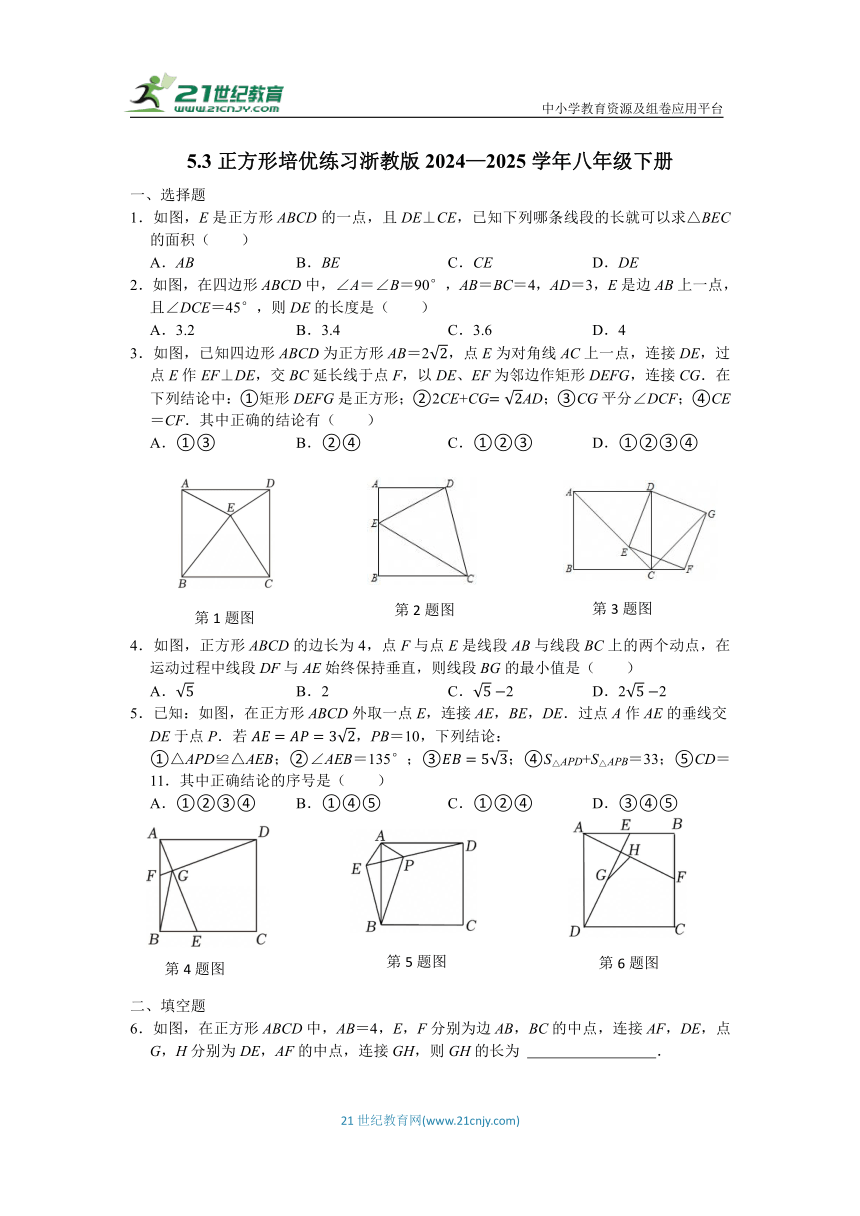
中小学教育资源及组卷应用平台 5.3正方形培优练习浙教版2024—2025学年八年级下册 一、选择题 1．如图，E是正方形ABCD的一点，且DE⊥CE，已知下列哪条线段的长就可以求△BEC的面积（　　） A．AB B．BE C．CE D．DE 2．如图，在四边形ABCD中，∠A＝∠B＝90°，AB＝BC＝4，AD＝3，E是边AB上一点，且∠DCE＝45°，则DE的长度是（　　） A．3.2 B．3.4 C．3.6 D．4 3．如图，已知四边形ABCD为正方形AB＝2，点E为对角线AC上一点，连接DE，过点E作EF⊥DE，交BC延长线于点F，以DE、EF为邻边作矩形DEFG，连接CG．在下列结论中：①矩形DEFG是正方形；②2CE+CGAD；③CG平分∠DCF；④CE＝CF．其中正确的结论有（　　） A．①③ B．②④ C．①②③ D．①②③④ 4．如图，正方形ABCD的边长为4，点F与点E是线段AB与线段BC上的两个动点，在运动过程中线段DF与AE始终保持垂直，则线段BG的最小值是（　　） A． B．2 C．2 D．22 5．已知：如图，在正方形ABCD外取一点E，连接AE，BE，DE．过点A作AE的垂线交DE于点P．若，PB＝10，下列结论： ①△APD≌△AEB；②∠AEB＝135°；③；④S△APD+S△APB＝33；⑤CD＝11．其中正确结论的序号是（　　） A．①②③④ B．①④⑤ C．①②④ D．③④⑤ 二、填空题 6．如图，在正方形ABCD中，AB＝4，E，F分别为边AB，BC的中点，连接AF，DE，点G，H分别为DE，AF的中点，连接GH，则GH的长为 　 　． 7．如图，点B、C分别在两条直线y＝2x和y＝kx上，点A、D是x轴上两点，已知四边形ABCD是正方形，则k值为　 　． 8．如图，平面直角坐标系中正方形ABCD的顶点A（0，12），B（5，0），过D作DF⊥x轴交AC于点E，连接BE，则△BEF的周长是 　 　． 9．如图，在正方形ABCD中，O是对角线AC，BD的交点，过点O作OE⊥OF分别交AB，BC于E，F两点，AE＝6，CF＝2，则EF的长为 　 　． 三、解答题 10．如图1，四边形ABCD为正方形，E为对角线AC上一点，连接DE，BE． （1）求证：BE＝DE； （2）如图2，过点E作EF⊥DE，交边BC于点F，以DE，EF为邻边作矩形DEFG，连接CG． ①求证：矩形DEFG是正方形； ②若正方形ABCD的边长为9，CG＝3，求正方形DEFG的边长． 11．如图，已知正方形ABCD中，E为CB延长线上一点，且BE＝AB，M、N分别为AE、BC的中点，连DE交AB于O，MN交，ED于H点． （1）求证：AO＝BO； （2）求证：∠HEB＝∠HNB； （3）过A作AP⊥ED于P点，连BP，则的值． 12．如图，在正方形ABCD中，E，F分别为AD，CD边上的中点，AF和BE相交于点P． （1）求证：AF⊥BE； （2）求证：∠DPF＝45°； （3）求证：PD2＝PA PB． 13．如图，已知正方形ABCD，AB＝4，点M在边CD上，射线AM交BD于点E，交射线BC于点F，过点C作CP⊥CE，交AF于点P． （1）求证：△ADE≌△CDE． （2）判断△CPF的形状，并说明理由． （3）作DM的中点N，连结PN，若PN＝3，求CF的长． 14．如图，正方形ABCD中，E是CD边的中点，F是BC边上一点，∠FAE＝∠DAE． （1）求证：AF＝AD+CF； （2）已知正方形ABCD的边长为4． ①求AF之长； ②若P是AE上一点，且△DEP是等腰三角形，则线段EP的长为 　 　． 参考答案 一、选择题 题号 1 2 3 4 5 答案 C B A D C 1．【解答】解：作EF⊥BC于F，EG⊥CD于G． ∴CD＝BC，∠BCD＝90°， ∴四边形EFCG为矩形， ∴CG＝EF， △BEC的面积等于． 当已知AB的长，AB＝BC，E是动点，EF的长是个变量，不能求出△BEC的面积，选项A错误． 当已知BE的长，E在以B为圆心，BE为半径的圆上，随E的位置变化，EF的长是变的，BC的长不知道，不能求出△BEC的面积，选项B错误，不符合题意． ∠CED＝90°，EG是斜边上的高， ∴∠CED＝∠CGE＝90°，∠CEG＝∠CDE， ∴△ECG∽△DCE， ∴CE2＝CG CD． ∴△BEC的面积．选项C正确，符合题意． 由选项C可知，同理可得：． ... ...