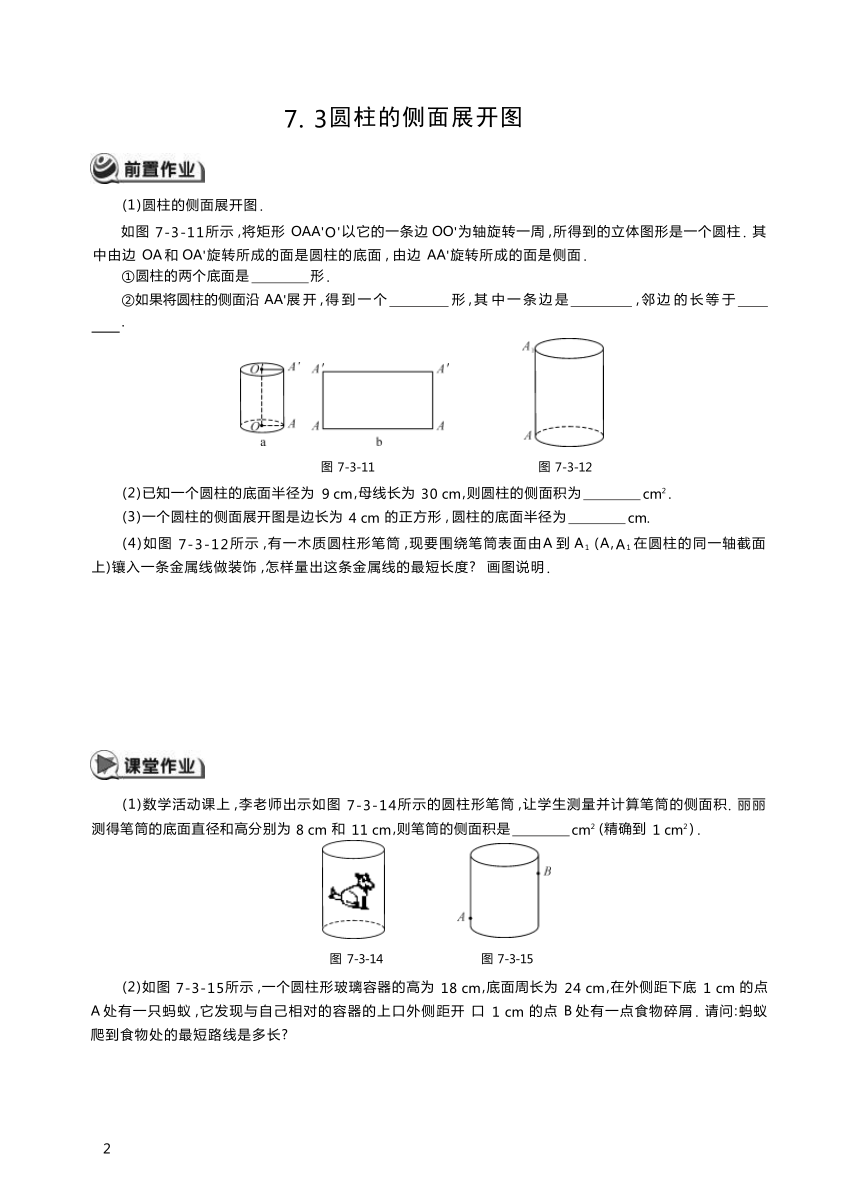
7. 3圆柱的侧面展开图 (1)圆柱的侧面展开图 . 如图 7-3-11所示 ,将矩形 OAA'O'以它的一条边 OO'为轴旋转一周 ,所得到的立体图形是一个圆柱 . 其 中由边 OA 和 OA'旋转所成的面是圆柱的底面 , 由边 AA'旋转所成的面是侧面 . ①圆柱的两个底面是 形 . ②如果将圆柱的侧面沿 AA'展 开 , 得 到 一 个 形 , 其 中 一 条 边 是 , 邻 边 的 长 等 于 . 图 7-3-11 图 7-3-12 (2)已知一个圆柱的底面半径为 9 cm ,母线长为 30 cm ,则圆柱的侧面积为 cm2 . (3)一个圆柱的侧面展开图是边长为 4 cm 的正方形 , 圆柱的底面半径为 cm. (4)如图 7-3-12所示 ,有一木质圆柱形笔筒 ,现要围绕笔筒表面由A 到 A1 (A,A1 在圆柱的同一轴截面 上)镶入一条金属线做装饰 ,怎样量出这条金属线的最短长度 画图说明 . (1)数学活动课上 ,李老师出示如图 7-3-14所示的圆柱形笔筒 ,让学生测量并计算笔筒的侧面积. 丽丽 测得笔筒的底面直径和高分别为 8 cm 和 11 cm ,则笔筒的侧面积是 cm2 (精确到 1 cm2 ) . 图 7-3-14 图 7-3-15 (2)如图 7-3-15所示 ,一个圆柱形玻璃容器的高为 18 cm ,底面周长为 24 cm ,在外侧距下底 1 cm 的点 A 处有一只蚂蚁 ,它发现与自己相对的容器的上口外侧距开 口 1 cm 的点 B 处有一点食物碎屑 . 请问:蚂蚁 爬到食物处的最短路线是多长 基础训练 (1)一个圆柱的侧面积与它的两个底面积之和相等 ,这个圆柱的高与底面直径的比是( ) . (2)一个圆柱的底面直径扩大 2倍 ,高不变 , 圆柱的侧面积( ) . A. 扩大到原来的 2倍 B. 缩小到原来的 C. 不变 D. 扩大到原来的 4倍 (3)一个圆柱的底面直径为 2 cm ,高为 4 cm , 圆柱的侧面积为( ) . A.8πcm2 B.16πcm2 C. 17πcm2 πcm2 (4)一个圆柱的底面半径为 3 cm ,高为 2 cm ,它的体积为( ) . A.97π cm3 B.18π cm3 C.3π cm3 D.18π2 cm3 拓展提高 (1)一个底面半径为 2 cm ,高为 3 cm 的圆柱的表面积是( ) . A.8π cm2 B.12π cm2 C.16π cm2 D.20π cm2 (2)用两张全等的矩形纸片分别卷成两个形状不同的柱面(圆柱的侧面) . 设较高圆柱的侧面积和底面 半径分别为 S1 和 r1 ,较矮圆柱的侧面积和底面半径分别为 S2 和 r2 ,那么( ) . A.S1 =S2 ,r1 =r2 B.S1 =S2 ,r1 >r2 C.S1 =S2 ,r1
~~ 您好,已阅读到文档的结尾了 ~~