第六章 平面向量 复习课教学设计

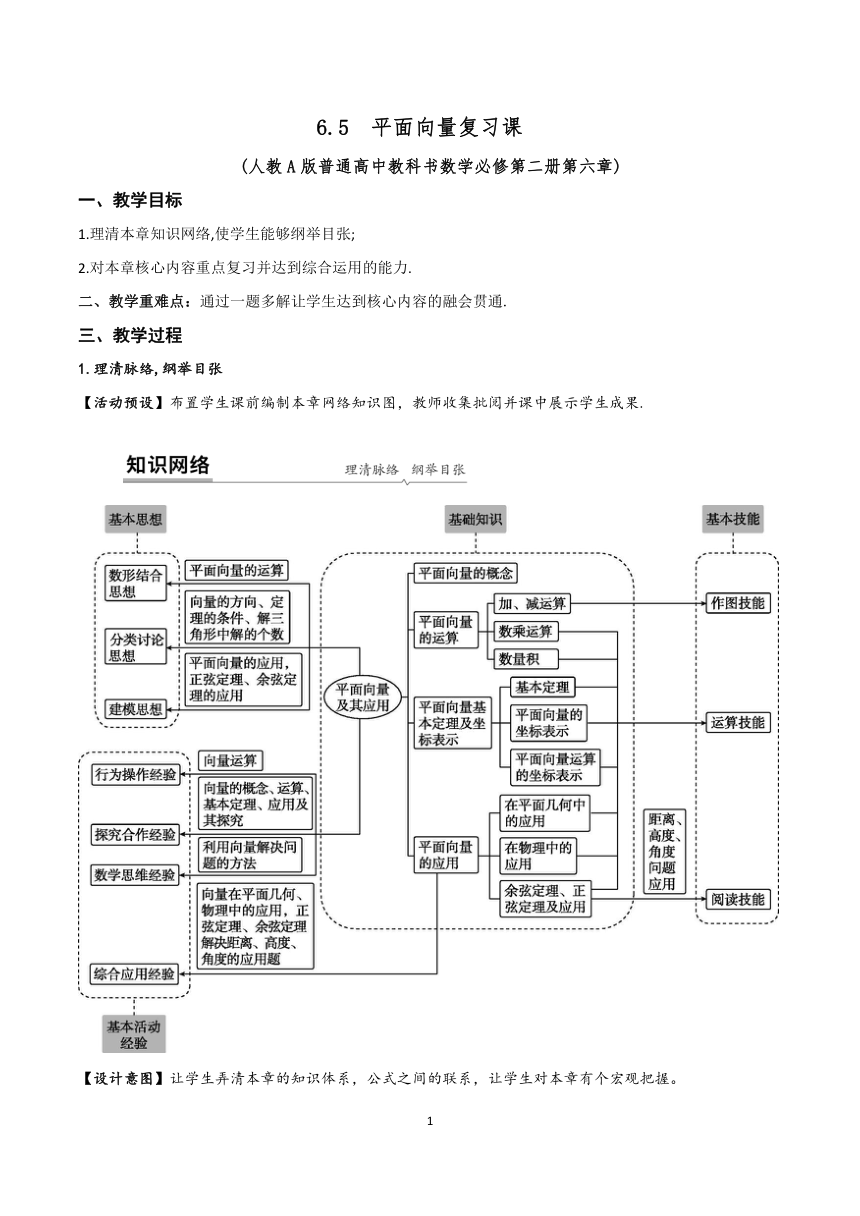
6.5 平面向量复习课 (人教A版普通高中教科书数学必修第二册第六章) 一、教学目标 1.理清本章知识网络,使学生能够纲举目张; 2.对本章核心内容重点复习并达到综合运用的能力. 二、教学重难点：通过一题多解让学生达到核心内容的融会贯通. 三、教学过程 1.理清脉络,纲举目张 【活动预设】布置学生课前编制本章网络知识图，教师收集批阅并课中展示学生成果. 【设计意图】让学生弄清本章的知识体系，公式之间的联系，让学生对本章有个宏观把握。 2.抓住核心,突破重点 典例1 【平面向量的最值问题】在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上.若，则的最大值为( ) A．3 B．2 C． D．2 【活动预设】先由学生独立思考，再由老师引导学生从特值法、坐标法、等和线法，找到解决问题的突破口，最后由老师展示解答过程，强调解题的关键点。 【解法1】特值法 ，,故选A 【小结】特值法，特立独行！ 【答案】A 【解析】由题意，画出右图． 设与切于点，连接． 以为原点，为轴正半轴， 为轴正半轴建立直角坐标系， 则点坐标为． ∵，． ∴． ∵切于点． ∴⊥． ∴是中斜边上的高． 即的半径为． ∵在上． ∴点的轨迹方程为． 设点坐标，可以设出点坐标满足的参数方程如下： 而，，． ∵ ∴，． 两式相加得： (其中，) 当且仅当，时，取得最大值3． ，若满足， 则，，所以， 设，即，点在圆上， 所以圆心到直线的距离，即，解得， 所以的最大值是 ，即的最大值是，故选A. 【小结】解析法，用数据说话！ 【小结】等和线法，等你来和一把！ 【知识拓广1】等和线的概念及其性质 1.等和线：平面内一组基底OA, OB 及任一向量OP,OP OA OB , R ，若点 P在直线 AB 上或在平行于 AB 的直线上，则 k (定值) ,反之也成立，我们把直线 AB 以及与直线 AB 平行的直线称为等和线. 2.等和线性质 ①当等和线恰为直线 AB 时， k 1 ； ②当等和线在O 点和直线 AB 之间时， k 0,1 ； ③当直线 AB 在O 点和等和线之间时， k 1, ； ④当等和线过O 点时， k 0 ； ⑤若两等和线关于O 点对称，则它们定值 k1,k2 互为相反数； ⑥定值 k 的变化与等和线到O 点的距离成正比； 3.等和线性质应用背景:在平面向量基本定理的表达式中，若需研究两系数的和时，可以用等值线法. 4.跟踪练习：　给定两个长度为1的平面向量和，它们的夹角为.如图所示，点C在以O为圆心的上运动．若，其中x，y∈R，求x＋y的最大值． ＝x＋y 常规解法：　以O为坐标原点，所在的直线为x轴建立平面直角坐标系，如图所示， 则A(1,0)，B.设∠AOC＝α，则C(cos α，sin α) 由＝x＋y，得所以x＝cos α＋sin α，y＝sin α 所以x＋y＝cos α＋sin α＝2sin，又α∈，所以当α＝时，x＋y取最大值2 等和线法：连AB,平移AB并使此线与圆弧相切,此时切点为圆弧中点E,连AE、BE,易知OAEB为平行四边形,此时＝＋,x＋y有最大值2. 【设计意图】解法1：特值法，四两拨千斤，化难为易！解法2：解析法，用数据说话，降低思维量！解法3：等和线法，在移动中联通彼岸！通过一题多解,融会贯通平面向量最值问题的解题技巧,并拓宽学生的知识面。 典例2【平面向量的数量积问题】已知是边长为2的等边三角形，P为平面ABC内一点，则的最小值是（ ） A. B. C. D. 【活动预设】先由学生独立思考完成该题，小组之间可以互相讨论，再由老师引导学生从坐标法、基底法、定义法、极化恒等式法，找到解决问题的突破口，最后由老师展示解答过程，强调解题的关键点。 【解法1】（坐标法） 如图建系： 设点 点为中，可以有两种思路： 【小结】本题由于是在等边三角形中的问题，可以考虑用坐标法解决.把所求的向量内积转化成坐标形式，进一步求出最小值. 【解法2】(基底转换法) ,当点与重合时=,等号成立. 【小结】基底表示法是 ... ...