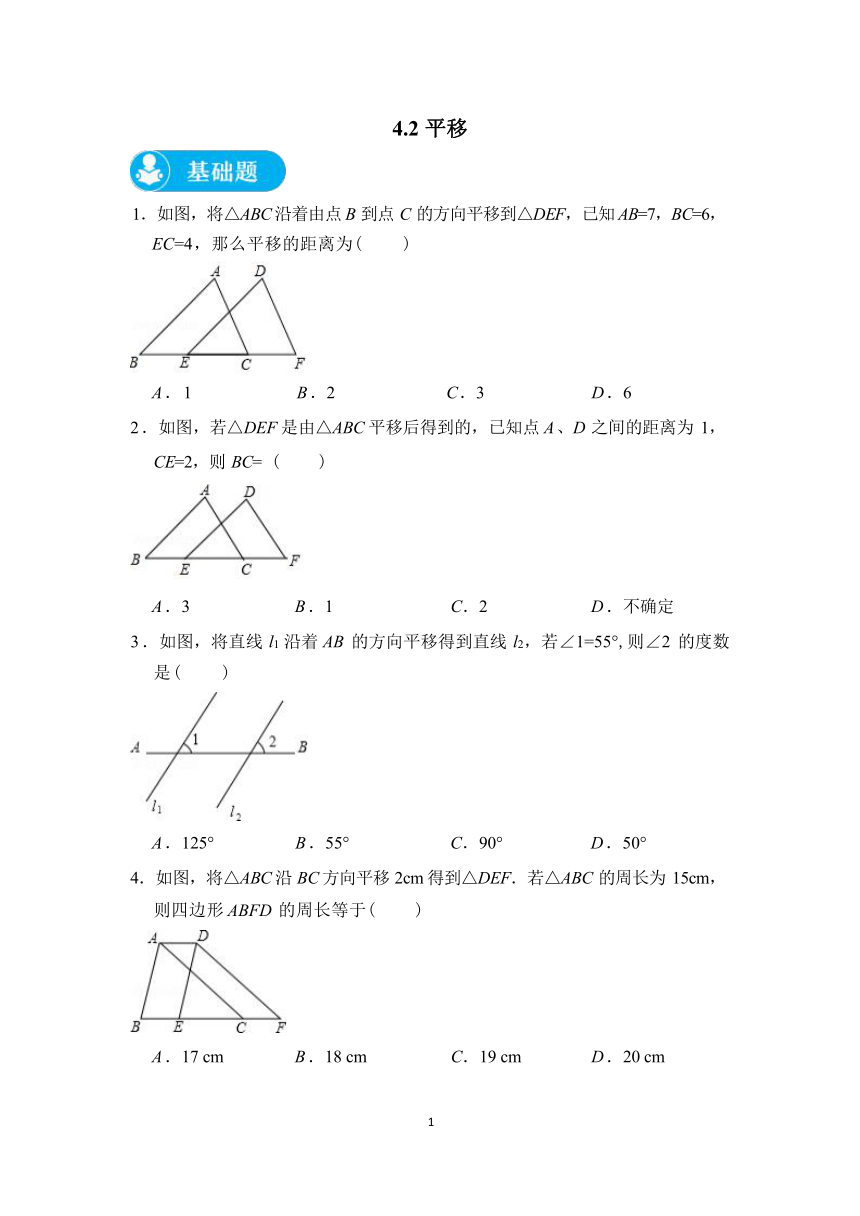
4.2 平移 1.如图,将△ABC 沿着由点 B 到点 C 的方向平移到△DEF,已知 AB=7,BC=6, EC=4,那么平移的距离为( ) A . 1 B .2 C .3 D .6 2 .如图,若△DEF 是由△ABC 平移后得到的,已知点 A 、D 之间的距离为 1, CE=2,则 BC= ( ) A .3 B .1 C.2 D .不确定 3 .如图,将直线 l1 沿着 AB 的方向平移得到直线 l2,若∠1=55°,则∠2 的度数 是( ) A .125° B .55° C.90° D .50° 4.如图,将△ABC 沿 BC 方向平移 2cm 得到△DEF.若△ABC 的周长为 15cm, 则四边形 ABFD 的周长等于( ) A .17 cm B .18 cm C.19 cm D .20 cm 1 5 .如图,图中是重叠的两个直角三角形.现将其中一个直角三角形沿 BC 方向 平移得到△DEF.如果 AB=9cm,BE=4cm,DH=3cm,则图中阴影部分面积为 2 cm . 6 .如图,将△ABE 向右平移 3cm 得到△DCF,如果△ABE 的周长是 12cm,那 么四边形 ABFD 的周长是 cm. 7 .如图,将△ABC 沿射线 BC 方向平移到△A'B'C'的位置.若 BC'=17 ,B'C=5, 则 BB'的长为 . 8.已知△ABC,AB=3cm,将△ABC沿着AB方向平移得到△A,B,C,,已知A,B=lcm, 则 CC,= cm. 9 .如图,将△ABC 沿 BC 方向平移 1 个单位得到△DEF,若△ABC 的周长等于 10cm,则四边形 ABFD 的周长等于 . 2 10 .在平面直角坐标系中,△ABC 的三个项点的位置如图所示,现将△ABC 沿 AA'的方向平移,使得点 A 移至图中的点 A'的位置. (1)在直角坐标系中,画出平移后所得△A'B'C'(其中 B, 、C'分别是 B 、C 的对 应点) (2)(1)中所得的点 B, ,C,的坐标分别是 . 11 .如图,将△ABC 沿直线 BC 向右平移到△A1B1 C1 的位置,延长 AC、A1B1 相 交于点 D. (1)求证:∠A=∠D; (2)请写出图中 3 条不同类型的正确结论. 12 .如图,在△ABC 中,AB=6cm ,BC=4cm,AC=3cm .将△ABC 沿着与 AB 垂 直的方向向上平移 3cm,得到△DEF. (1)四边形 ABDF 是什么四边形? (2)求阴影部分的面积? 3 13.如图,在正方形网格中建立平面直角坐标系,已知点 A(3,2),(4 , -3), C(1 , -2),请按下列要求操作: (1)请在图中画出△ABC; (2)将△ABC 向左平移 5 个单位长度,再向上平移4 个单位长度,得到△A1B1 C1, 在图中画出△A1B1 C1 ,并直接写出点 A1 、B1 、C1 的坐标. 14 .如图,在边长为 1 个单位长度的小正方形组成的 8×8 网格中,三角形 ABC 的三个均在格点上,将三角形 ABC 向左平移 3 个单位长度、再向下平移 2 个 单位长度得到三角形 DEF. (1)画出平移后的三角形 DEF; (2)若点 A 向左平移 n 个单位长度在三角形 DEF 的内部,请直接写出所有符合 条件的整数 n 的值. 4 参考答案 1 .B 【分析】观察图象,发现平移前后,B 、E 对应,C、F 对应,根据平移的性质, 易得平移的距离=BE=6 -4=2,进而可得答案. 【解答】解:根据平移的性质, 易得平移的距离=BE=6 -4=2 , 故选:B. 2 .A 【分析】根据平移的性质,结合图形可直接求解. 【解答】解: 观察图形可知:△DEF 是由△ABC 沿 BC 向右移动 BE 的长度后得 到的,根据对应点所连的线段平行且相等,得 BE=AD=1. 所以 BC=BE+CE=1+2=3, 故选:A. 3 .B 【解答】解:∵l1 ∥l2, ∴∠2=∠1, ∵∠1=55° , ∴∠2=55° , 故选:B. 4 .C 【分析】根据平移的性质可得 DF=AC,再求出四边形 ABFD 的周长等于△ABC 的周长加上 AD 与 CF,然后计算即可得解. 【解答】解:∵△ABC 沿 BC 方向平移 2cm 得到△DEF, ∴DF=AC,AD=CF=2cm, ∴四边形 ABFD 的周长=AB+BF+DF+AD =AB+BC+CF+AC+AD =△ABC 的周长+AD+CF =15+2+2 =19cm. 5 故选:C. 5 .30 【分析】根据平移的性质可得到相等的边与角,再根据 S△ABC -S△HEC=S△DEF -S △HEC,即 S 阴 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

