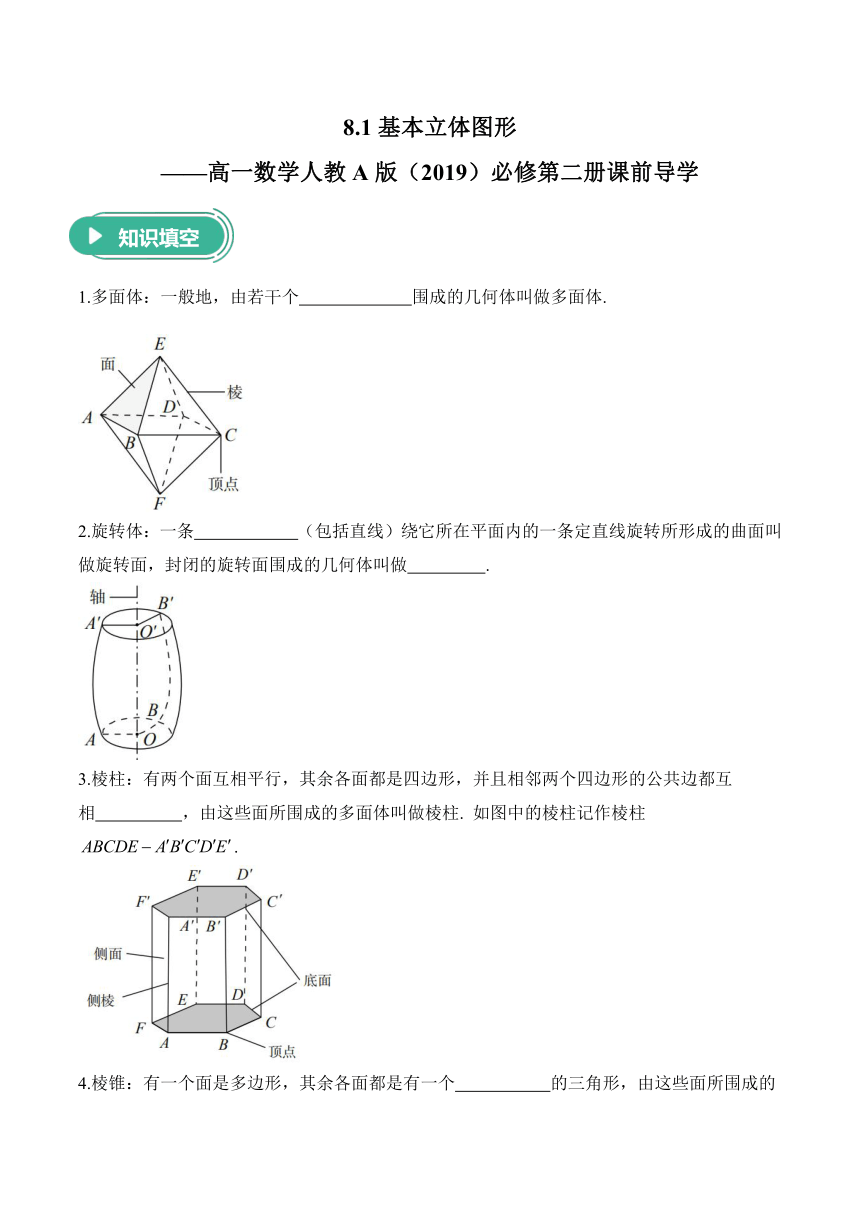
8.1基本立体图形 高一数学人教A版（2019）必修第二册课前导学（含答案）

8.1基本立体图形 ———高一数学人教A版（2019）必修第二册课前导学 知识填空 1.多面体：一般地，由若干个 围成的几何体叫做多面体. 2.旋转体：一条 （包括直线）绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面，封闭的旋转面围成的几何体叫做 . 3.棱柱：有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相 ，由这些面所围成的多面体叫做棱柱. 如图中的棱柱记作棱柱. 4.棱锥：有一个面是多边形，其余各面都是有一个 的三角形，由这些面所围成的多面体叫做棱锥. 如图中的棱锥记作棱锥. 5.棱台：用一个平行于棱锥底面的平面去截棱锥，底面和截面之间那部分多面体叫做 .如图中的棱台记作棱台. 6.圆柱：以矩形的一边所在直线为旋转轴，其余三边旋转 形成的面所围成的旋转体叫做圆柱. 如图中的圆柱记作圆柱. 7.圆锥：以直角三角形的一条 所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体叫做圆锥. 如图中的圆锥记作圆锥. 8.圆台：用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做 . 如图中的圆台记作圆台. 9.球：半圆以它的直径所在直线为旋转轴，旋转一周形成的 叫做球面，球面所围成的旋转体叫做 ，简称球. 如图中的球记作球O. 10.简单组合体：由简单几何体组合而成的几何体. 简单组合体的构成有两种基本形式：一种是由简单几何体 而成；一种是由简单几何体 或挖去一部分而成. 思维拓展 1.棱柱结构特征问题的解题策略有哪些？ 2.简单旋转体判断问题的解题策略是什么？ 3.多面体展开图问题的解题策略有哪些？ 基础练 习 1.“棱柱的相邻两个侧面是矩形”是“该棱柱为直棱柱”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件 2.有下列四个说法，其中正确的是( ) A.圆柱的母线与轴垂直 B.圆锥的母线长等于底面圆直径 C.圆台的母线与轴平行 D.球的直径必过球心 3.下面几何体的截面一定是圆面的是( ) A.圆锥 B.球 C.圆柱 D.棱柱 4.下列说法正确的是( ) A.空间中，到一个定点的距离等于定长的点的集合是球 B.以直角三角形一边为旋转轴旋转所得的旋转体是圆锥 C.用一个平面去截圆锥，得到一个圆锥和一个圆台 D.棱柱的侧棱都相等，侧面都是平行四边形 5.如图所示的平面图形可以折叠成的立体图形为( ) A.三棱锥 B.四棱柱 C.四棱锥 D.球 【答案及解析】 一、知识填空 1.平面多边形 2.平面曲线 旋转体 3.平行 4.公共顶点 5.棱台 6.一周 7.直角边 8.圆台 9.曲面 球体 10.拼接 截去 二、思维拓展 二、问题思考 1.（1）有关棱柱概念辨析问题应紧扣棱柱定义： ①两个面互相平行； ②其余各面是四边形； ③相邻两个四边形的公共边互相平行.求解时，首先看是否有两个面平行，再看是否满足其他特征. （2）多注意观察一些实物模型和图片便于反例排除. 2.（1）准确掌握圆柱、圆锥、圆台和球的生成过程及其结构特征是解决此类概念问题的关键. （2）解题时要注意两个明确：明确由哪个平面图形旋转而成；明确旋转轴是哪条直线. 3.（1）绘制展开图：绘制多面体的表面展开图要结合多面体的几何特征，发挥空间想象能力或者是亲手制作多面体模型.在解题过程中，常常给多面体的顶点标上字母，先把多面体的底面画出来，然后依次画出各侧面，便可得到其表面展开图. （2）由展开图复原几何体：若是给出多面体的表面展开图，来判断是由哪一个多面体展开的，则可把上述过程逆推.同一个几何体的表面展开图可能是不一样的，也就是说，一个多面体可有多个表面展开图. 三、基础练习 1.答案：C 解析：若棱柱的相邻两个侧面是矩形，则两侧面的交线必定垂直于底面，所以该棱柱为直棱柱，满足充分性；若棱柱为直棱柱，则棱柱的相邻两个侧面是矩形，满足必要性.故“棱柱的相邻两个侧面是矩形 ... ...