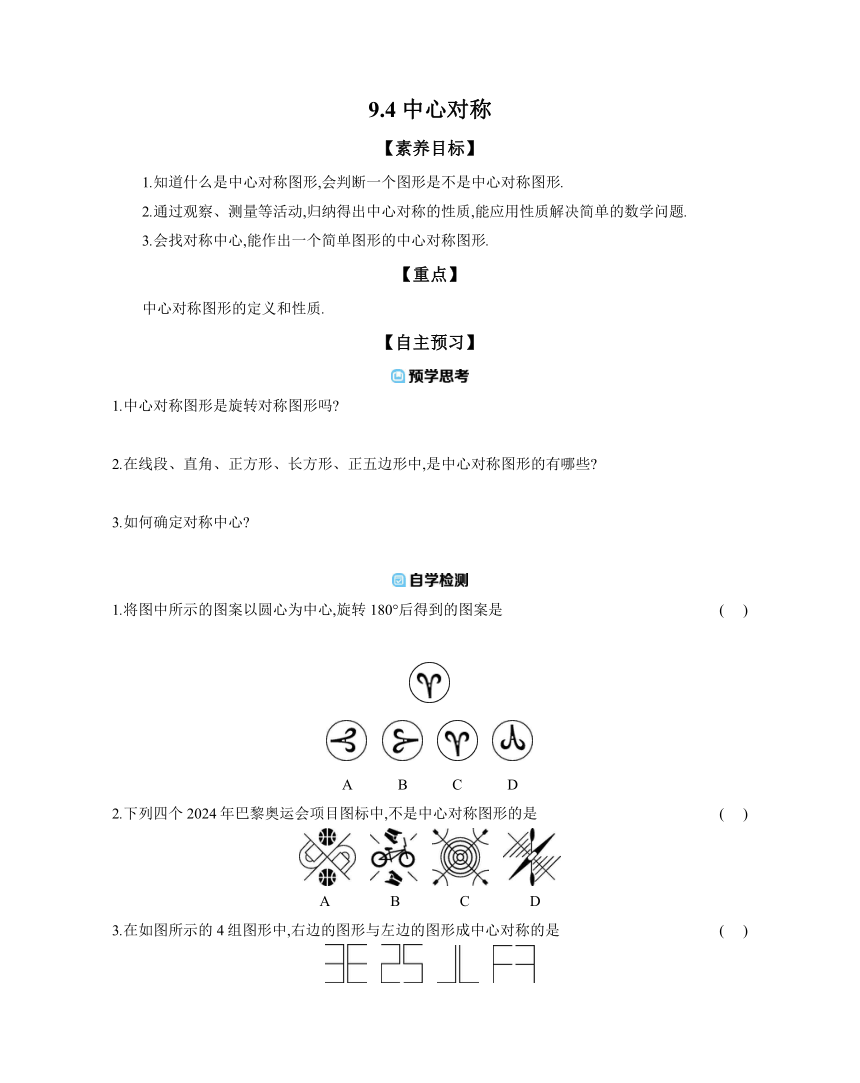
9.4 中心对称 【素养目标】 1.知道什么是中心对称图形,会判断一个图形是不是中心对称图形. 2.通过观察、测量等活动,归纳得出中心对称的性质,能应用性质解决简单的数学问题. 3.会找对称中心,能作出一个简单图形的中心对称图形. 【重点】 中心对称图形的定义和性质. 【自主预习】 1.中心对称图形是旋转对称图形吗 2.在线段、直角、正方形、长方形、正五边形中,是中心对称图形的有哪些 3.如何确定对称中心 1.将图中所示的图案以圆心为中心,旋转180°后得到的图案是 ( ) A B C D 2.下列四个2024年巴黎奥运会项目图标中,不是中心对称图形的是 ( ) A B C D 3.在如图所示的4组图形中,右边的图形与左边的图形成中心对称的是 ( ) A B C D 【参考答案】 预学思考 1.是. 2.线段、正方形、长方形. 3.连结两组对应点,交点是对称中心. 自学检测 1.D 2.B 3.A 【合作探究】 中心对称图形和中心对称的概念 请你阅读课本本节开始至“探索”上面的内容,思考:什么样的图形是中心对称图形 两个图形满足什么特点时成中心对称 【观察图片】1.观察下面的图片,它们是旋转对称图形吗 2.如果是的话,它们各需要至少旋转多少度与自身重合 3.如图,△ABC绕点O旋转180度后与△A'B'C'重合,则点A的对应点是 ,BC的对应线段是 . 【得出定义】1.一个图形绕着中心旋转180度后能与自身重合,我们把这种图形叫做 . 2.把一个图形绕着某一点旋转 度,如果它能够与另一个图形重合,我们就说这两个图形成 ,这个点叫做对称中心,这两个图形的对应点叫做 . 【举例说明】你能举出生活中中心对称图形或中心对称的实例吗 【深入讨论】1.中心对称图形与旋转对称图形有什么联系 2.中心对称图形和中心对称有什么区别 1.在下列图形中,是中心对称图形的是 ( ) A B C D 中心对称的性质 请你阅读课本“探索”至“做一做”的内容,思考:中心对称有哪些性质 【观察图形】1.请你完成课本“探索”中的问题. 2.你还能得到哪些相等的线段 【归纳性质】在成中心对称的两个图形中,连结对称点的线段都经过 ,并且被对称中心 .反过来,如果两个图形的 所有对应点连成的线段都经过某一点,并且被该点 ,那么这两个图形关于这一点成 . 2.如图,若四边形ABCD与四边形FGCE成中心对称,则它们的对称中心是点 ,点A的对称点是点 ,点E的对称点是点 ,BD∥ ,且BD= ,连结A,F的线段经过点 ,且被点C . 作中心对称图形 例 图1、图2均为7×6的正方形方格,点A,B,C在格点上. (1)在图1中确定格点D,并画出一个以A,B,C,D为顶点的四边形,使其为轴对称图形. (2)在图2中确定格点E,并画出一个以A,B,C,E为顶点的四边形,使其为中心对称图形. 变式训练 如图,已知四边形ABCD和点E,作出与四边形ABCD关于点E成中心对称的四边形A'B'C'D'. 【参考答案】 知识点一 观察图片 1.是. 2.180度. 3.点A' 线段B'C' 得出定义 1.中心对称图形 2.180 中心对称 关于中心的对称点 举例说明 答案不唯一,学生举例只要正确即可,如中国结等. 深入讨论 1.中心对称图形是旋转对称图形的一种特殊情况,是旋转角为180度的旋转对称图形. 2.中心对称图形是一个图形所具有的特殊性质,中心对称是两个图形之间的关系. 对点训练 1.C 知识点二 观察图形 1.点B,O,B',点C,O,C',OB',OC'. 2.AB=A'B',BC=B'C',CA=C'A'. 归纳性质 对称中心 平分 平分 中心对称 对点训练 2.C F D EG EG C 平分 题型精讲 例 解:如图所示. 变式训练 解:如图所示. ... ...
~~ 您好,已阅读到文档的结尾了 ~~