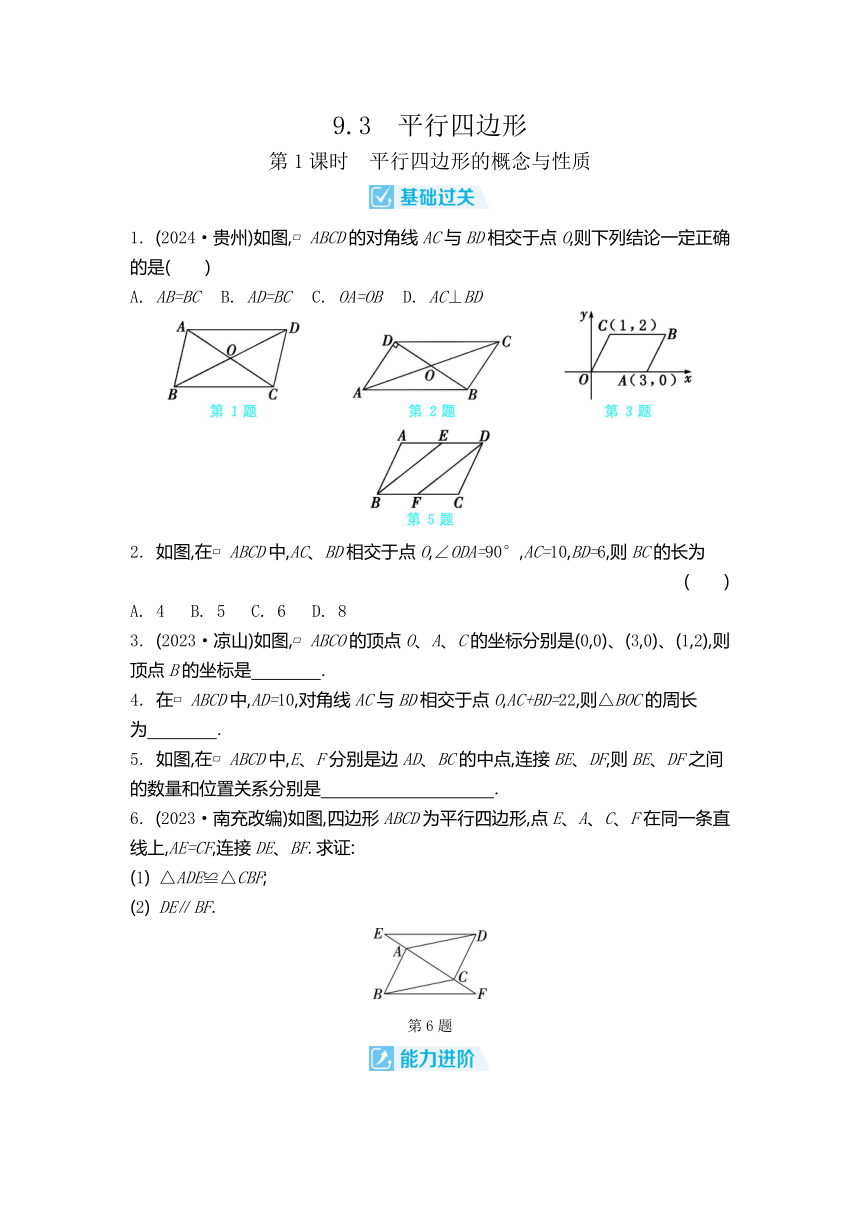
9.3 平行四边形 第1课时 平行四边形的概念与性质 1. (2024·贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( ) A. AB=BC B. AD=BC C. OA=OB D. AC⊥BD 2. 如图,在 ABCD中,AC、BD相交于点O,∠ODA=90°,AC=10,BD=6,则BC的长为 ( ) A. 4 B. 5 C. 6 D. 8 3. (2023·凉山)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是 . 4. 在 ABCD中,AD=10,对角线AC与BD相交于点O,AC+BD=22,则△BOC的周长为 . 5. 如图,在 ABCD中,E、F分别是边AD、BC的中点,连接BE、DF,则BE、DF之间的数量和位置关系分别是 . 6. (2023·南充改编)如图,四边形ABCD为平行四边形,点E、A、C、F在同一条直线上,AE=CF,连接DE、BF.求证: (1) △ADE≌△CBF; (2) DE∥BF. 第6题 第7题 7. (2024·眉山)如图,在 ABCD中,O为BD的中点,EF经过点O.有下列结论:① AB∥DC;② EO=ED;③ ∠A=∠C;④ S四边形ABOE=S四边形CDOF.其中,一定正确的有 ( ) A. 1个 B. 2个 C. 3个 D. 4个 8. 如图,将 ABCD沿对角线BD折叠,使点A落在点E处.若∠1=56°,∠2=42°,则∠C的度数为 ( ) A. 108° B. 109° C. 110° D. 111° 9. (2023·福建改编)如图,在 ABCD中,O为对角线BD上一点,EF过点O,且分别交AB、CD于点E、F.若OD=BD,OE=10,则EF的长为 . 10. 在平面直角坐标系中, ABCD的顶点A、C、D的坐标分别是(-1,2)、(2,-1)、(3,2),则顶点B的坐标是 . 11. 已知四边形ABCD是平行四边形,AB=6,∠BAD的平分线交直线BC于点E.若CE=2,则 ABCD的周长为 . 12. 如图,在 ABCD中,点E、F分别在AD、BC上,且ED=FB,连接AF、CE.求证:四边形AFCE是平行四边形. 第12题 13. 如图,在 ABCD中,∠BCD=120°,分别延长DC、BC到点E、F,连接AE、BE、AF、DF,使△BCE和△CDF都是等边三角形. (1) 求证:AE=FA; (2) 求∠EAF的度数. 第13题 第2课时 由对边的关系判定平行四边形 1. 如图,在四边形ABCD中,∠A=100°,∠B=80°,添加下列条件,不能判定四边形ABCD是平行四边形的为 ( ) A. ∠C=100° B. ∠D=80° C. AB∥CD D. AD∥BC 2. 如图,E是 ABCD的边AD的延长线上一点,连接BE、CE、BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是 ( ) A. ∠ABD=∠DCE B. DF=CF C. ∠AEB=∠BCD D. ∠AEC=∠CBD 3. 如图,在四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.请你只添加一个条件: (不另加辅助线),使得四边形AECF为平行四边形. 4. 如图,在 ABCD中,∠BAD=120°,连接BD,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F,且CF=1,则AB的长为 . 5. (2024·武汉改编)如图,在 ABCD中,点E、F分别在边BC、AD上,AF=CE,连接EF、AE、CF. (1) 求证:△ABE≌△CDF. (2) 当点E在线段BC的什么位置时,四边形ABEF是平行四边形 为什么 第5题 6. 在四边形ABCD中,有下列条件:① AB∥CD;② AD∥BC;③ AB=CD;④ AD=BC.从中选择两个条件,使四边形ABCD为平行四边形的选法共有 ( ) A. 3种 B. 4种 C. 5种 D. 6种 第7题 7. (2024·辽宁)如图, ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD,DE、CE相交于点E.若AC=3,BD=5,则四边形OCED的周长为( ) A. 4 B. 6 C. 8 D. 16 8. 在平面直角坐标系中,有四个点O(0,0)、A(3,0)、B(1,1)、C(x,1),则当x的值为 时,以O、A、B、C为顶点的四边形是平行四边形. 9. 如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺画出△ABD的边BD上的中线(不写作法,保留作图痕迹). 10. 如图,∠DBC=90°,四边形ABCD是平行四边形吗 为什么 第10题 11. 如图,在 ABCD中,E、F分别为边AD、BC的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~