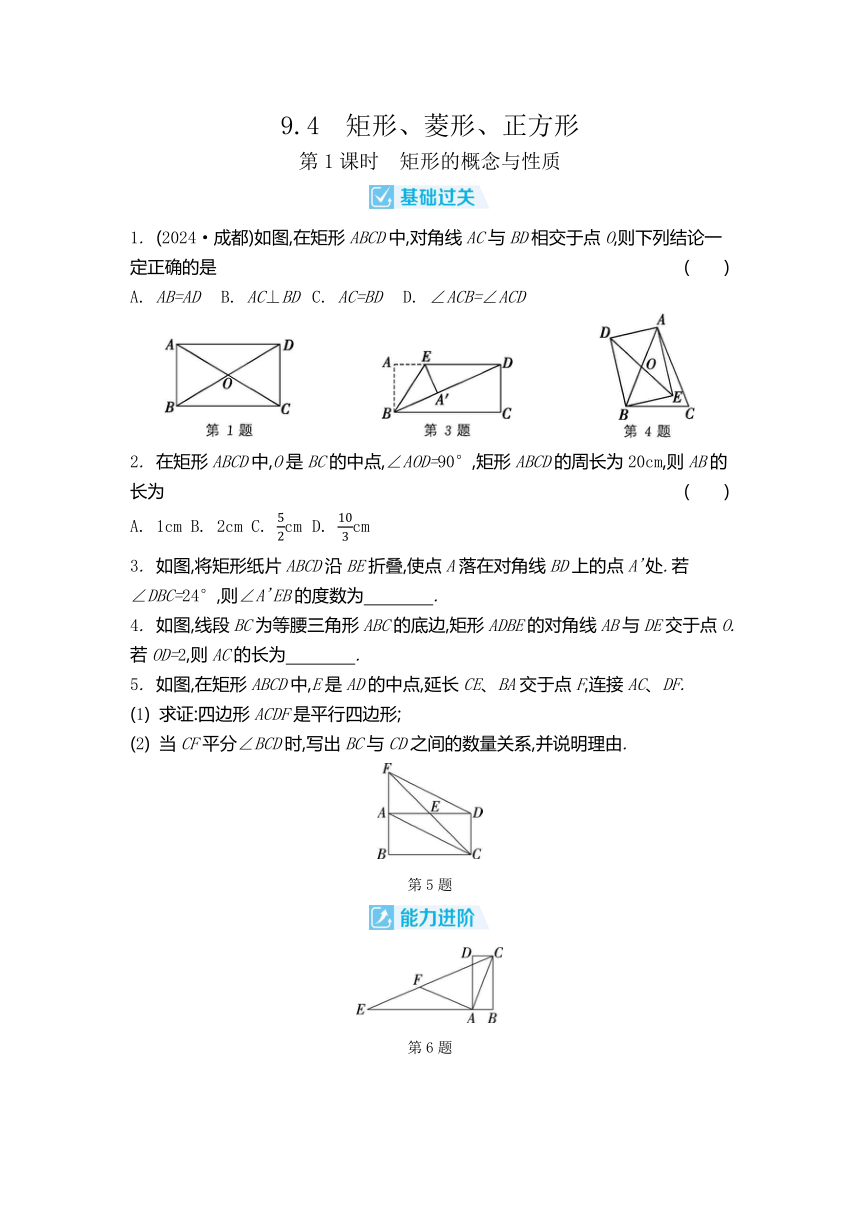
9.4 矩形、菱形、正方形 第1课时 矩形的概念与性质 1. (2024·成都)如图,在矩形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( ) A. AB=AD B. AC⊥BD C. AC=BD D. ∠ACB=∠ACD 2. 在矩形ABCD中,O是BC的中点,∠AOD=90°,矩形ABCD的周长为20cm,则AB的长为 ( ) A. 1cm B. 2cm C. cm D. cm 3. 如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的点A'处.若∠DBC=24°,则∠A'EB的度数为 . 4. 如图,线段BC为等腰三角形ABC的底边,矩形ADBE的对角线AB与DE交于点O.若OD=2,则AC的长为 . 5. 如图,在矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF. (1) 求证:四边形ACDF是平行四边形; (2) 当CF平分∠BCD时,写出BC与CD之间的数量关系,并说明理由. 第5题 第6题 6. 如图,在矩形ABCD中,E是BA的延长线上一点,F是CE上一点,连接AC、AF.若AC=AF=EF,∠ACB=21°,则∠ECD的度数为 ( ) A. 7° B. 21° C. 23° D. 24° 7. (2023·哈尔滨)矩形ABCD的对角线AC、BD相交于点O,点F在矩形ABCD的边上,连接OF.若∠ADB=38°,∠BOF=30°,则∠AOF的度数为 . 第8题 8. 如图,在矩形ABCD中,AB=6,BC=10,以点B为圆心,BC的长为半径画弧,交AD于点E,连接BE,再分别以点C、E为圆心,大于CE的长为半径画弧,两弧交于点F,作射线BF交CD于点G,则CG的长为 . 9. (2023·宿迁改编)如图,在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F. (1) 求证:AE=CF; (2) 当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,图中面积等于矩形ABCD面积的的三角形是 . 第9题 10. 如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),a、b满足+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动. (1) 点B的坐标为 .当点P移动3.5秒时,点P的坐标为 . (2) 当点P到x轴的距离为4个单位长度时,求点P的移动时间. (3) 当以O、B、P为顶点的三角形的面积为10时,求点P的移动时间. 第10题 第2课时 矩形的判定 1. (2024·泸州)已知四边形ABCD是平行四边形,则添加下列一个条件后,不能判定 ABCD为矩形的是 ( ) A. ∠A=90° B. ∠B=∠C C. AC=BD D. AC⊥BD 2. 下列说法正确的是 ( ) A. 有两个角是直角的四边形是矩形 B. 有三个直角的四边形是矩形 C. 对角线相等的四边形是矩形 D. 对角线互相平分的平行四边形是矩形 3. 如图,在 ABCD中,对角线BD=8cm,AE⊥BD,垂足为E,且AE=3cm,BC=4cm,则AD与BC之间的距离为 cm. 4. 如图,工人师傅砌墙时,要想检验门框ABCD是否符合设计要求(即门框是否为矩形),在确保两组对边分别平行的前提下,只要测量出对角线AC、BD的长度,然后看它们是否相等就可以判断了. (1) 当AC BD时,门框符合要求(填“=”或“≠”); (2) 这种做法的依据是 . 5. (2023·贵州)如图,在Rt△ABC中,∠ACB=90°,延长CB至点D,使得BD=CB,过点A、D分别作AE∥BD,DE∥BA,AE与DE相交于点E,连接BE、CE.求证:BE⊥CD,CE=DE. 第5题 第6题 6. 如图,在 ABCD中,对角线AC、BD相交于点O,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是 ( ) A. OM=AC B. MB=MO C. BD⊥AC D. ∠AMB=∠CND 第8题 7. 设AB、CD、EF是同一平面内三条互相平行的直线.已知AB与CD之间的距离是12cm,EF与CD之间的距离是5cm,则AB与EF之间的距离是 . 8. 如图,在矩形ABCD中,AB=6,AD=8,且有一点P从点B出发,沿着BD往点D移动,过点P作AB的垂线,交AB于点E,过点P作AD的垂线,交AD于点F,连接EF,则EF长的最小值为 . 9. (2024·贵州)如图,四边形ABCD的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

