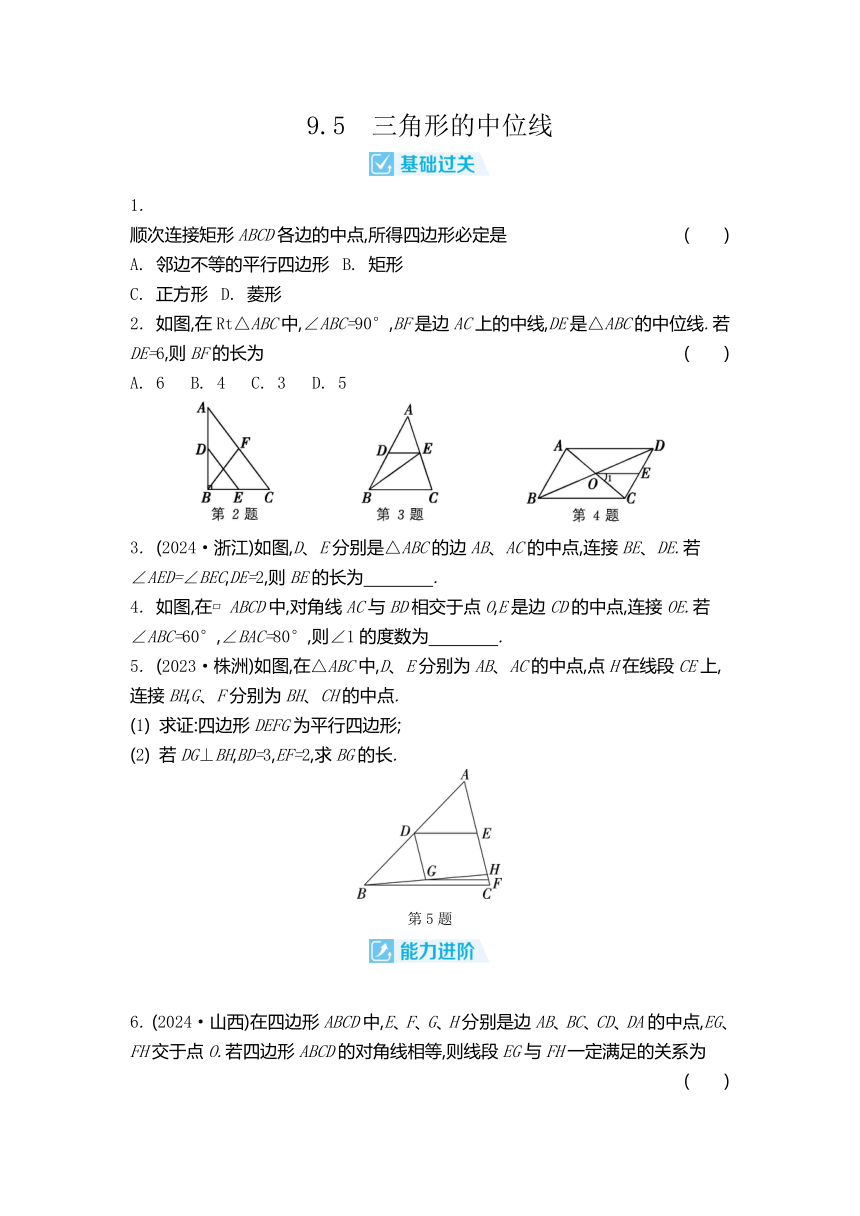
9.5 三角形的中位线 1. 顺次连接矩形ABCD各边的中点,所得四边形必定是 ( ) A. 邻边不等的平行四边形 B. 矩形 C. 正方形 D. 菱形 2. 如图,在Rt△ABC中,∠ABC=90°,BF是边AC上的中线,DE是△ABC的中位线.若DE=6,则BF的长为 ( ) A. 6 B. 4 C. 3 D. 5 3. (2024·浙江)如图,D、E分别是△ABC的边AB、AC的中点,连接BE、DE.若∠AED=∠BEC,DE=2,则BE的长为 . 4. 如图,在 ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=60°,∠BAC=80°,则∠1的度数为 . 5. (2023·株洲)如图,在△ABC中,D、E分别为AB、AC的中点,点H在线段CE上,连接BH,G、F分别为BH、CH的中点. (1) 求证:四边形DEFG为平行四边形; (2) 若DG⊥BH,BD=3,EF=2,求BG的长. 第5题 6. (2024·山西)在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,EG、FH交于点O.若四边形ABCD的对角线相等,则线段EG与FH一定满足的关系为 ( ) A. 互相垂直平分 B. 互相平分且相等 C. 互相垂直且相等 D. 互相垂直平分且相等 第7题 7. (2023·泸州)如图, ABCD的对角线AC、BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,连接OE.若AD=4,CD=6,则EO的长为 ( ) A. 1 B. 2 C. 3 D. 4 8. 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数为 . 9. 如图,△ABC的周长为19,点D、E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M.若BC=7,则MN的长为 . 10. 如图,在△ABC中,AB=13,BC=12,D、E分别是AB、BC的中点,连接DE、CD.若DE=2.5,则△ACD的周长是多少 第10题 11. (2023·枣庄)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=7,F为DE的中点,若△CEF的周长为32,求OF的长. 第11题 12. (2024·新疆)如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点,连接DE、EF、FG、GD. (1) 求证:四边形DEFG是平行四边形; (2) 若BD=CE,求证:四边形DEFG是矩形. 第12题 9.5 三角形的中位线 1. D 2. A 3. 4 4. 40° 5. (1) ∵ D、E分别为AB、AC的中点,G、F分别为BH、CH的中点,∴ DE是△ABC的中位线,GF是△HBC的中位线.∴ DE∥BC,DE=BC,GF∥BC,GF=BC.∴ DE∥GF,DE=GF.∴ 四边形DEFG为平行四边形 (2) ∵ 四边形DEFG为平行四边形,∴ DG=EF=2.∵ DG⊥BH,∴ ∠DGB=90°.∴ 在Rt△BGD中,BG=== 6. A 7. A 8. 18° 9. 10. ∵ D、E分别是AB、BC的中点,DE=2.5,∴ DE是△ABC的中位线.∴ AC=2DE=5.∵ AB=13,BC=12,∴ AC2+BC2=52+122=169,AB2=132=169.∴ AC2+BC2=AB2.∴ ∠ACB=90°.在Rt△ABC中,∵ D是AB的中点,∴ AD=CD=AB=6.5.∴ △ACD的周长=AC+AD+CD=18 11. ∵ 四边形ABCD是正方形,∴ ∠BCD=90°,BC=DC,BO=DO. ∵ 在Rt△DCE中,F为DE的中点,∴ CF=EF=DF=DE.∵ CE=7,△CEF的周长为32,∴ DE=25.∴ 在Rt△DCE中,DC===24.∴ BE=BC-CE=DC-CE=17.∵ BO=DO,F为DE的中点,∴ OF是△DBE的中位线.∴ OF=BE= 12. (1) ∵ BD、CE是△ABC的中线,∴ D、E分别是AC、AB的中点.∴ DE是△ABC的中位线.∴ DE∥BC,DE=BC.同理,可得FG∥BC,FG=BC.∴ DE∥FG,DE=FG.∴ 四边形DEFG是平行四边形 (2) 由(1),知四边形DEFG是平行四边形.∴ OF=OD.又∵ F是OB的中点,∴ BF=OF.∴ DF=BD.同理,可得EG=CE.∵ BD=CE,∴ DF=EG.∵ 四边形DEFG是平行四边形,∴ 四边形DEFG是矩形 ... ...
~~ 您好,已阅读到文档的结尾了 ~~