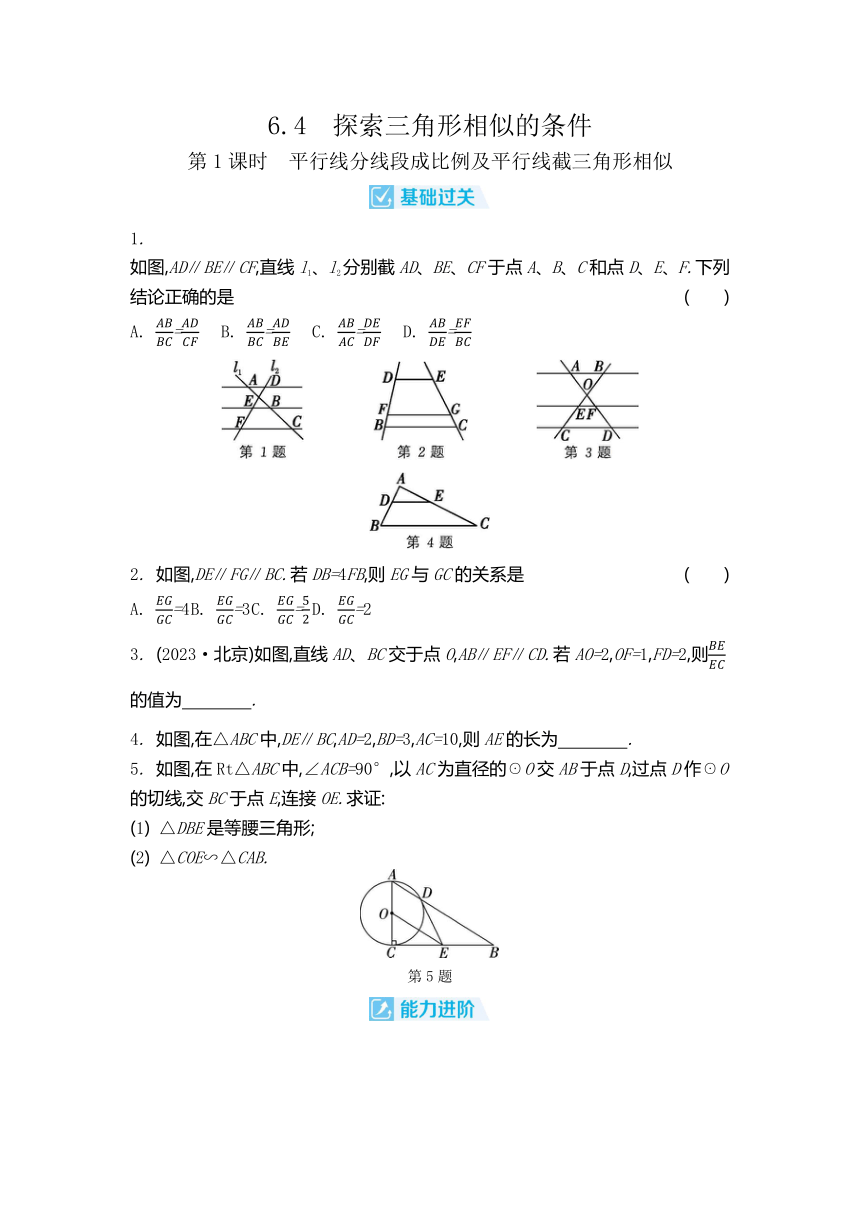
6.4 探索三角形相似的条件 第1课时 平行线分线段成比例及平行线截三角形相似 1. 如图,AD∥BE∥CF,直线l1、l2分别截AD、BE、CF于点A、B、C和点D、E、F.下列结论正确的是 ( ) A. = B. = C. = D. = 2. 如图,DE∥FG∥BC.若DB=4FB,则EG与GC的关系是 ( ) A. =4 B. =3 C. = D. =2 3. (2023·北京)如图,直线AD、BC交于点O,AB∥EF∥CD.若AO=2,OF=1,FD=2,则的值为 . 4. 如图,在△ABC中,DE∥BC,AD=2,BD=3,AC=10,则AE的长为 . 5. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O交AB于点D,过点D作☉O的切线,交BC于点E,连接OE.求证: (1) △DBE是等腰三角形; (2) △COE∽△CAB. 第5题 第6题6. 如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,M为边BC上一点(不与点B、C重合),连接AM交DE于点N,则下列结论正确的是 ( ) A. = B. = C. = D. = 7. (2024·陕西)如图,正方形CEFG的顶点G在正方形ABCD的边CD上,AF与DC交于点H.若AB=6,CE=2,则DH的长为 ( ) A. 2 B. 3 C. D. 8. 如图,AD是△ABC的中线,AE=EF=FC,BE交AD于点G,连接DF,则的值为 . 9. (2023·岳阳)如图,在☉O中,AB为直径,BD为弦,C为的中点,连接AC,交BD于点F,以C为切点的切线与AB的延长线交于点E,连接CD.若=,则的值为 . 10. 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6. (1) 直接指出图中所有的相似三角形; (2) 求DE的长. 第10题 11. 如图,在△ABC中,D是AC的中点,△ABC的角平分线AE交BD于点F,交BC于点E.若BF∶FD=3∶1,AB+BE=3,求△ABC的周长. 第11题 第2课时 用两角的关系判定三角形相似 1. 如图,D、E、F、G四点分别在△ABC的三边上,其中DG与EF相交于点H.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是 ( ) A. △BDG和△CEF B. △ABC和△EFC C. △ABC和△BDG D. △FGH和△ABC 2. 有下列图形:① 两个等边三角形;② 两个顶角为40°的等腰三角形;③ 两个底角为40°的等腰三角形.其中,一定相似的有 ( ) A. 0组 B. 1组 C. 2组 D. 3组 3. (2023·大庆)如图,点N在矩形纸片ABCD的边AD上,现将矩形折叠,折痕为BN,点A的对应点为M.若点M恰好落在边DC上,则图中与△NDM一定相似的三角形是 . 4. 如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 . 5. (2024·德阳)如图,在菱形ABCD中,∠ABC=60°,对角线AC与BD相交于点O,F为BC的中点,连接AF与BD相交于点E,连接CE并延长,交AB于点G.求证:△BEF∽△BCO. 第5题 第6题 6. (2023·恩施)如图,在△ABC中,DE∥BC,分别交AC、AB于点D、E,EF∥AC,交BC于点F,且=,BF=8,则DE的长为 ( ) A. B. C. 2 D. 3 7. 如图①所示为一张等边三角形纸片ABC,点D在AB上,点E在BC上.如图②,现沿DE将点B往右折后,BD、BE分别与AC相交于点F、G.若AD=10,AF=16,DF=14,BF=8,则CG的长为 ( ) A. 7 B. 8 C. 9 D. 10 8. (2024·宜宾)如图,正五边形ABCDE的边长为4,则这个正五边形的对角线AC的长为 . 9. 如图,在正方形ABCD中,M是边BC上一定点,连接AM.请用尺规作图,在线段AM上作一点P,使△DPA∽△ABM(不写作法,保留作图痕迹). 10. (2024·无锡)如图,AB是☉O的直径,△ACD内接于☉O,=,AB、CD的延长线相交于点E,且DE=AD. (1) 求证:△CAD∽△CEA; (2) 求∠ADC的度数. 第10题 11. (2024·湖北)如图,在矩形ABCD中,AB=2,AD=3,点E、F分别在边AD、BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为G,PG交BC于点H.当P为CD的中点时,求GH的长. 第11题 第3课时 用两边及夹角的关系判定三角形相似 1. 如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿各选项中的虚线剪开,剪下的涂色三角形 ... ...
~~ 您好,已阅读到文档的结尾了 ~~