中考数学几何模型决胜88招模型63 相似之一线三垂直模型（含解析）

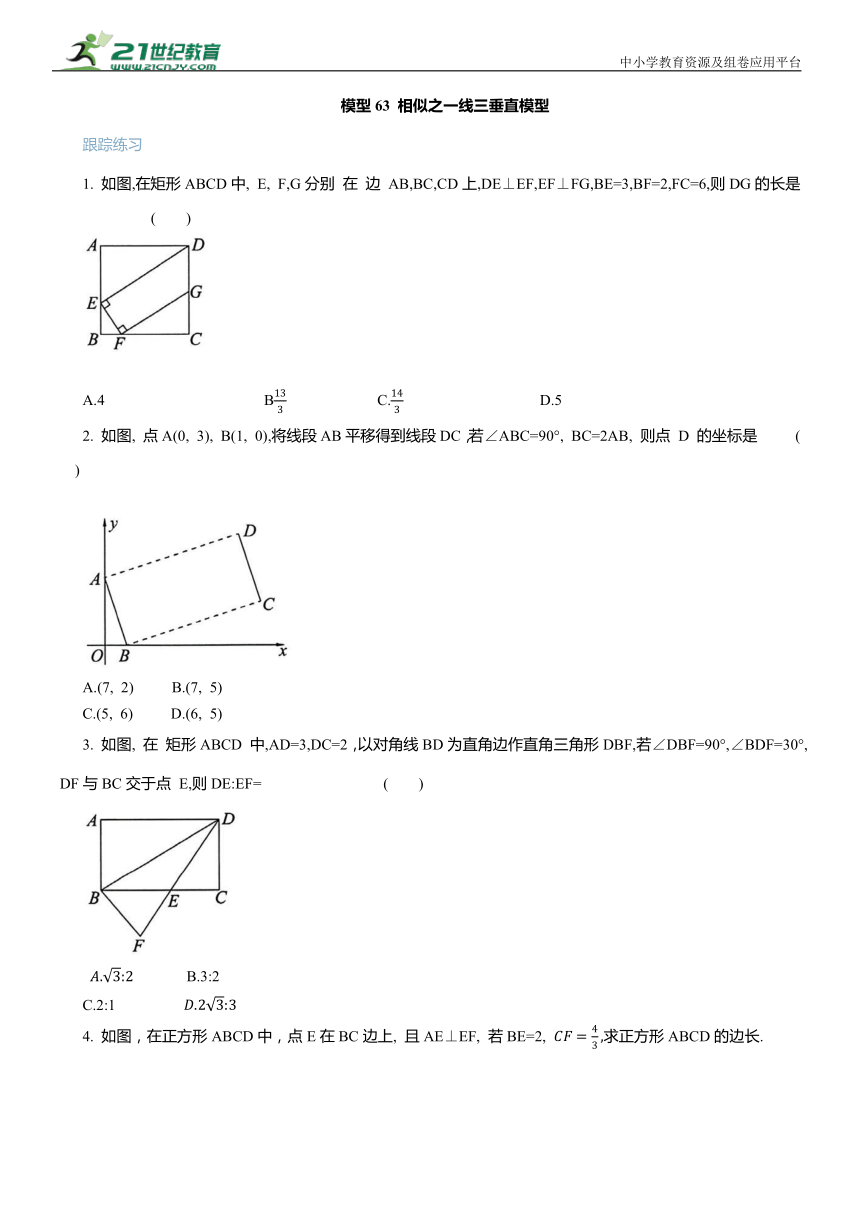
中小学教育资源及组卷应用平台 模型63 相似之一线三垂直模型 跟踪练习 1. 如图,在矩形ABCD中, E, F,G分别 在 边 AB,BC,CD上,DE⊥EF,EF⊥FG,BE=3,BF=2,FC=6,则DG的长是 ( ) A.4 B C. D.5 2. 如图, 点A(0, 3), B(1, 0),将线段AB平移得到线段DC，若∠ABC=90°, BC=2AB, 则点 D 的坐标是 ( ) A.(7, 2) B.(7, 5) C.(5, 6) D.(6, 5) 3. 如图, 在 矩形ABCD 中,AD=3,DC=2，以对角线BD为直角边作直角三角形DBF,若∠DBF=90°,∠BDF=30°, DF与BC交于点 E,则DE:EF= ( ) B.3:2 C.2:1 4. 如图，在正方形ABCD中，点E在BC边上, 且AE⊥EF, 若BE=2, 求正方形ABCD的边长. 5. 如图, 在矩形ABCD中, AB=4, AD=5, E,F，G，H分别为矩形边上的点，HF过矩形的中心O, 且HF=AD, E为AB的中点，G为CD的中点，则四边形 EFGH的周长为 ( ) B.6 C.8 6. 在△ABC中,∠BAC=90°, AB=AC, 直线l经过点A，过点B，C分别作l的垂线，垂足分别为点 D，E. (1)特例体验：如图1，若直线l∥ BC, AB=AC= 分别求出线段BD, CE和DE的长; (2)规律探究： ①如图2，若直线l从图1状态开始绕点A顺时针旋转α(0°<α<45°),请探究线段BD，CE和DE的数量关系并说明理由； ②如图3，若直线l从图1状态开始绕点A顺时针旋转α(45°<α<90°) , 与线段BC相交于点 H,请再探究线段 BD，CE和DE的数量关系并说明理由； (3)尝试应用：在图3中，延长线段BD交线段AC于点F,若CE=3,DE=1, 求 S△BFC· 1. B 解析: ∵ EF⊥ FG, ∴ ∠EFB+∠GFC=90°,∵四边形 ABCD为矩形,∴ ∠A=∠B=∠C=90°,AB=CD,AD=BC,∴ ∠GFC+∠FGC=90°,∴ ∠EFB=∠FGC,又∵ ∠B=∠C=90°,∴△EFB∽△FGC,∴BE=BF/G,∵ BE=3,BF=2,FC=6, 同 理 可得 故选B. 2. D 解析:过点D作DE⊥y轴于点E,如图, ∵ 点 A(0,3),B(1,0), ∴OA=3,OB=1. ∵将线段AB平移得到线段 DC, ∴ AB∥ CD,AB=CD,∴四边形ABCD是平行四边形, ∵∠ABC=90°, ∴四边形ABCD是矩形. ∴∠BAD=90°,BC=AD. ∵ BC=2AB, ∴A D =2 A B . ∵ ∠AO B =90°, ∴∠BAO+∠ABO=90°, 又∵∠BAO+∠DAE=90°, ∴∠ABO=∠EAD, 又∵∠AOB=∠AED=90°,∴△ABO∽△DAE. AE=2OB=2,∴OE=OA+AE=5,∴D(6,5).故选 D. 3. D 解析: 过点 F作 FG⊥AB, 交 AB的延长线于点 G，如图. ∵∠DBF=90°, ∠A=∠G=90°, ∴∠ABD+∠GBF=∠GBF+∠BFG=90°, ∴∠ABD=∠BFG,又∵∠A=∠G=90°,∴△ABD∽△GFB,∴∠AB=BDFB, ∵∠DBF=90°, ∠BDF=30°, ∴BG= ,∵GF∥BC∥AD,∴DE:EF= 故选D. 4. 解析: ∵ AE⊥EF, ∴∠AEB+∠CEF=90°, ∵四边形 ABCD为正方形, ∴AB=BC, ∠B=∠C=90°, ∴∠BAE+∠AEB=90°, ∴∠BAE=∠CEF, 又∵∠B=∠C=90°, ∴△CEF∽△BAE, 又∵ BE=2, ∴ CE=4, ∴ BC=CE+BE=4+2=6, ∴正方形ABCD的边长为6. 直击中考 5. B 解析: 如图, 连接EG, ∵四边形ABCD 是矩形, ∴ AB=CD, AB∥CD, ∵ E 为 AB 的中点, G 为 CD 的中点,∴ AE=DG, AE∥DG, ∴四边形AEGD是平行四边形, ∴ AD=EG. ∵矩形是中心对称图形，HF过矩形的中心O, ∴EG过点O, 且OH=OF, OE=OG,∴四边形 EHGF 是平行四边形, ∵ HF=AD, ∴EG=HF, ∴四边形EHGF是矩形,∴∠EHG=90°, ∵∠A=∠D=90°, ∴∠AHE+∠AEH=∠AHE+∠DHG=90°, ∴∠AEH=∠DHG, ∴△AEH ∽△DHG, 设AH=x, 则 DH=5-x, 又∵AE= 解得x=1或4, ∴ AH=1或4. 当AH=1时, DH=4,则 ∴四边形 EFGH的周长为 当AH=4时，同理可得 ∴四边形EFGH的周长为 6 ,故选B. 6. 解析: (1) 在△ABC中, ∠BAC=90°,AB=AC, ∴∠ABC=∠ACB=45°, ∵l∥BC, ∴∠DAB=∠ABC=45°,∠CAE=∠ACB=45°,又∵∠ADB=∠CEA=90°, ∴∠DAB=∠ABD=45°,∠EAC=∠ACE=45°, ∴ AD=BD, AE=CE, ∴ AD=BD=AE=CE=1, ∴ DE=2. (2)①DE=BD+CE. 理由如下: 在 Rt△ADB中, ∠ABD+∠BAD=90°, ∵ ∠BAC=90°, ∴∠BAD+∠CAE=90°, ∴ ... ...