2025年 中考数学复习--一次函数100题（含解析）

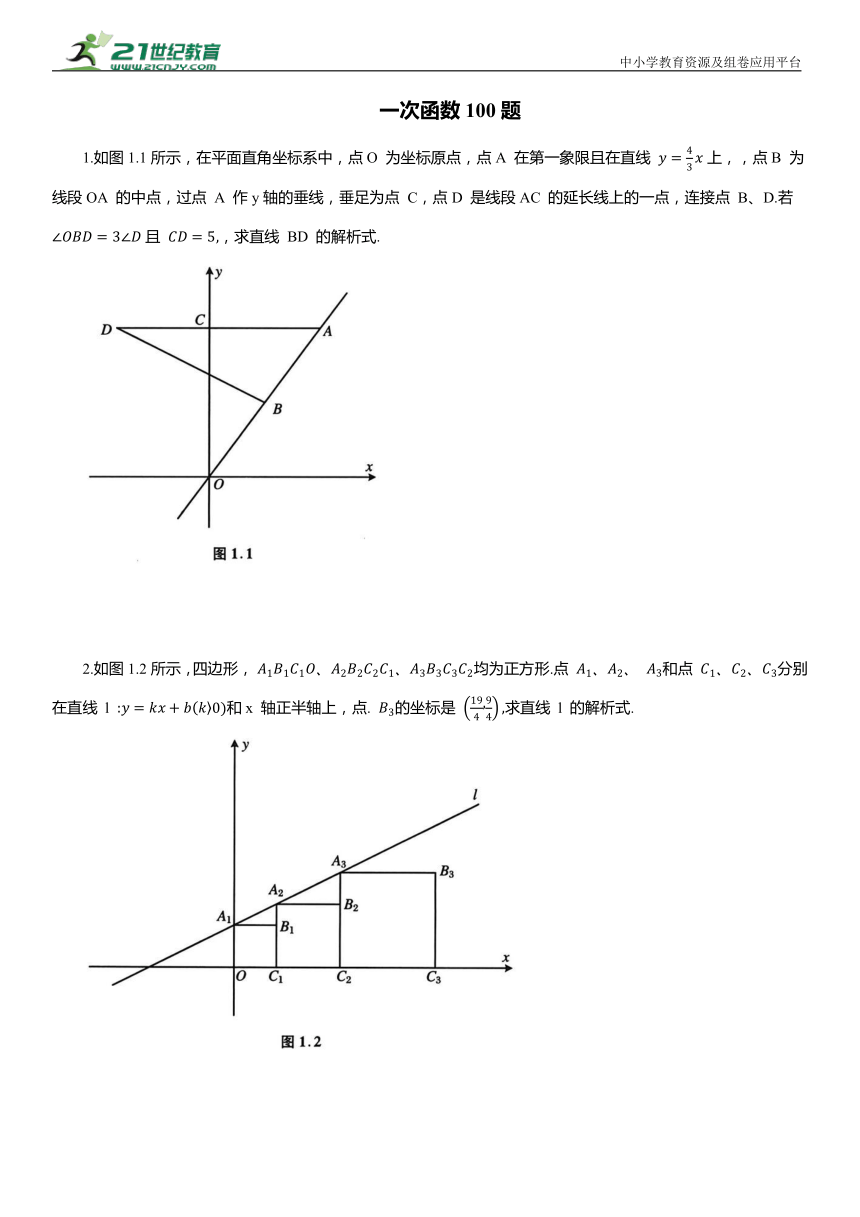
一次函数100题 1.如图1.1所示，在平面直角坐标系中，点O 为坐标原点，点A 在第一象限且在直线 上，，点B 为线段OA 的中点，过点 A 作y轴的垂线，垂足为点 C，点D 是线段AC 的延长线上的一点，连接点 B、D.若 且 ，求直线 BD 的解析式. 2.如图1.2所示，四边形， 均为正方形.点 和点 分别在直线 l 和x 轴正半轴上，点. 的坐标是 求直线 l 的解析式. 3.如图1.3所示，在平面直角坐标系xOy中，A为y轴正半轴上一点，B为x轴正半轴上一点， 光线从点 C(1,0)出发,到 AB 上一点E,经直线AB 反射后到AO 上一点D，经AO反射后回到点C，则点 E 的坐标为 . 4.如图1.4所示，直线 与x轴、y轴分别交于点A、B，直线 与x轴、y轴分别交于点C、D，点 E 为线段AB 上一点，且 求点 E 的坐标. 5.已知正比例函数 的图像经过A(-2,4)、B(1,b),如图1.5所示. (1) 求 k、b 的值. (2)若已知点 C(0，2)，试问：在坐标轴上是否存在一点 P，使 若存在，求出点P 的坐标；若不存在，请说明理由. 6.如图1.6 所示,直线 与 x 轴相交于点A，与y 轴相交于点B.直线 经过点A，与y轴相交于点C.在直线 AC 上是否存在点D，使 若存在，求点 D 的坐标；若不存在，请说明理由. 中小学教育资源及组卷应用平台 7.如图1.7所示，已知直线l： 交x轴于点A、交y轴于点B，点C 在线段OB 上运动(不与点 O、B 重合),连接点 A、C,作( 交线段AB 于点D. (1)求A、B两点的坐标. (2)当点 D 的纵坐标为8时，求点 C 的坐标. (3)过点 B 作直线BF⊥y轴,交 CD 的延长线于点F.设OC=m,BF=n,试求 n与m的函数关系式,并直接写出m、n的取值范围. 8.如图1.8所示,四边形 ABCO 为矩形,点 B 的坐标为(4,2),点 A 在y轴正半轴上,点C 在x轴正半轴上，点E为AB 边上的一点，坐标为(1，2)，点D为y轴负半轴上一动点，点 F 为x轴正半轴上一动点，且 在直线 上找点 P，使 试求出点 P 的坐标. 9.如图1.9所示，点A、B分别在一次函数. 的图像上，其横坐标分别为a、 .设直线 AB 的解析式为 若 是整数时，k也是整数，试求出满足条件的所有 k 值. 10.已知一次函数 的图像与x轴、y轴分别相交于点 A、B，1 2,点 P(a,b)在该函数的图像上. (1) 求 k 的值. (2)若点 P 到x轴、y轴的距离之和等于2，求点 P 的坐标. (3)设 ，如果在两个实数a 与b之间(不包括a 和b)有且只有一个整数，求实数 m 的取值范围. 11.已知一次函数的图像经过点 和 并且 (1)求此一次函数的解析式. (2)此一次函数的图像是否有可能经过横坐标和纵坐标都是整数的点 请给出你的理由. 12.在平面直角坐标系 xOy中，已知直线 与直线 交于点 A,l 与y轴交于点B,l 与y轴交于点C. (1)当点 A 在x轴上时,求 k 的值及点A、B的坐标. (2)横、纵坐标都是整数的点称为整点，记线段 BC、AC、AB 围成的区域(不含边界)为W，区域 W 内整点个数为n，结合函数图像回答： ①在(1)的条件下， ②若 直接写出 k 的取值范围： . 13.阅读材料：在平面直角坐标系中，任何直线的方程均可化为一般形式： C=0(其中A、B、C为常数系数).例如：直线方程 可变形为 一般地，我们在平面直角坐标系中求点到直线的距离，可用下面的公式求解： 点 到直线 的距离公式是 比如,求点 P(1,1)到直线. 的距离为 根据以上材料解答下列问题： (1) 求点 P(1,1)到直线. 的距离，并判断点 P 与直线的位置关系. (2)求点. 到直线 的距离. (3)求两条平行线 和 间的距离. (4)已知点 M(-1,3)与直线 上点N的距离是3，则 的面积是 . 14.问题：探究函数y=|x|-2的图像与性质. 小华根据学习函数的经验，对函数y=|x|-2的图像与性质进行了探究. 下面是小华的探究过程，请补充完整： (1)在函数 中，自变量x的取值范围是 . (2)表1.1所示是 y与x的几组对应值. 表1.1 x 99 -3 -2 -1 0 1 2 3 y 1 0 -1 -2 -1 0 m ②若A(n,2019)、B(2021,2019)为 ... ...