9.4 探索三角形相似的条件 解答专项练习题（含答案）鲁教版八年级数学下册

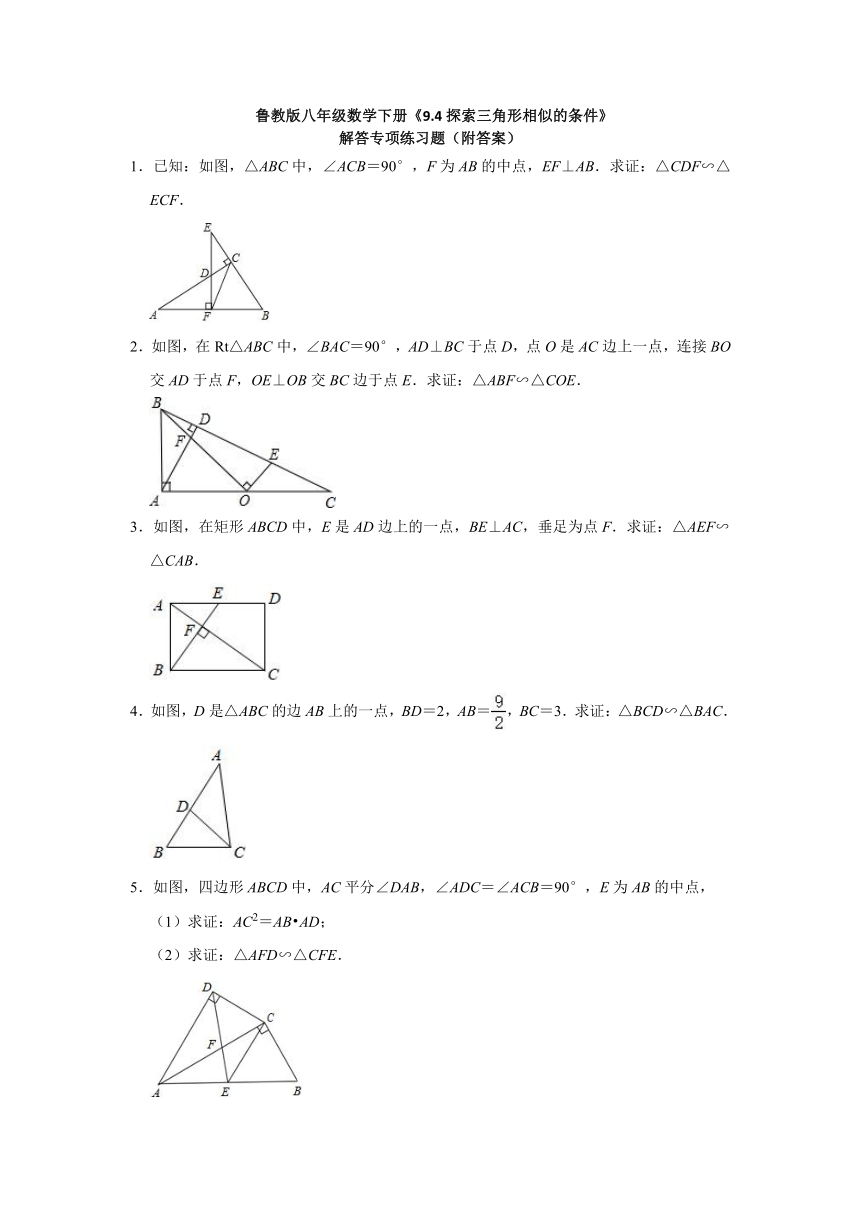
鲁教版八年级数学下册《9.4探索三角形相似的条件》 解答专项练习题（附答案） 1．已知：如图，△ABC中，∠ACB＝90°，F为AB的中点，EF⊥AB．求证：△CDF∽△ECF． 2．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于点F，OE⊥OB交BC边于点E．求证：△ABF∽△COE． 3．如图，在矩形ABCD中，E是AD边上的一点，BE⊥AC，垂足为点F．求证：△AEF∽△CAB． 4．如图，D是△ABC的边AB上的一点，BD＝2，AB＝，BC＝3．求证：△BCD∽△BAC． 5．如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点， （1）求证：AC2＝AB AD； （2）求证：△AFD∽△CFE． 6．如图，在Rt△ABC中，∠ACB＝90°，CD是边AB上的高，请指出其中一对相似三角形并证明之． 7．如图，在△ABC中，AB＝AC，BD＝CD，CE⊥AB于E．求证：△ABD∽△CBE． 8．阅读材料，回答问题 在边长为1的正方形ABCD中，E是AB的中点，CF⊥DE，F为垂足． （1）△CDF与△DEA是否相似？说明理由； （2）求CF的长． 9．如图，在△ABC中，CE⊥AB于点E，BD⊥AC于点D，连接ED，求证：△ABC∽△ADE． 10．如图，△ABC中，AB＝AC，D是BC中点，BE⊥AC于E，求证：△ACD∽△BCE． 11．如图，AD∥BC，AE平分∠DAB，BE平分∠ABC．EF⊥AB，证明：△AEF∽△ABE． 12．如图，在直角三角形ABC中，∠C＝90°，CD⊥AB，D是垂足，求证：△ACD∽△ABC． 13．如图，△ABC中，BE⊥AC于E，AD⊥BC于D．求证：△CDE∽△CAB． 14．已知：在Rt△ABC中∠C＝90°，CD为AB边上的高． 求证：Rt△ADC∽Rt△CDB． 15．在矩形ABCD中，F是BC上一点，AF的延长线交DC的延长线于G，DE⊥AG于E．根据上述条件，请在图中找出四组相似三角形，并说明其中一组的理由． 16．已知：如图，在△ABC中，∠ACB＝90°，过点C作CD⊥AB于点D，点E为AC上一点，过E点作AC的垂线，交CD的延长线于点F，与AB交于点G．求证：△ABC∽△FGD． 17．已知：正方形ABCD中，E、F分别是边CD、DA上的点，且CE＝DF，AE与BF交于点M． （1）求证：△ABF≌△DAE； （2）求证：△AMF∽△ADE； （3）观察判断BF与AE有怎样的位置关系？ 18．如图，在Rt△ABC中，CD是斜边AB上的中线，DF⊥AB，交AC于E，交BC的延长线于点F． （1）求证：∠A＝∠F； （2）△CDE与△FDC是否相似？并给予证明． 19．如图，正方形AEFG的顶点E在正方形ABCD的边CD上，AD的延长线交EF于H点． （1）试说明：△AED∽△EHD； （2）若E为CD的中点，正方形ABCD的边长为4，求DH的长． 20．已知：正方形ABCD中，E、F分别是边CD、DA上的点，且CE＝DF，AE与BF交于点M． （1）求证：△ABF≌△DAE； （2）找出图中与△ABM相似的所有三角形（不添加任何辅助线）． 21．已知Rt△ABC中，直角边AC＝3，BC＝4，P、Q分别是AB、BC上的动点，且点P不与A、B重合．点Q不与B、C重合． （1）若CP⊥AB于点P，如图1，△CPQ为等腰三角形，这时满足条件的点Q有几个？直接写出相等的腰和相应的CQ的长（不写解答过程） （2）当P是AB的中点时，如图2，若△CPQ与△ABC相似，这时满足条件的点Q有几个？分别求出相应的CQ的长？ 参考答案 1．证明：∵△ABC中，∠ACB＝90°，F为AB的中点， ∴AF＝CF，∠A+∠B＝90°． ∴∠A＝∠DCF． ∵EF⊥AB， ∴∠B+∠E＝90°， ∴∠A＝∠E， ∴∠E＝∠DCF， ∴△CDF∽△ECF． 2．证明：∵AD⊥BC， ∴∠DAC+∠C＝90°．　　　（2分） ∵∠BAC＝90°， ∴∠BAF＝∠C．　　　（2分） ∵OE⊥OB， ∴∠BOA+∠COE＝90°．　　（2分） ∵∠BOA+∠ABF＝90°， ∴∠ABF＝∠COE．　　　　　　（2分） ∴△ABF∽△COE．　　　　　　（2分） 3．证明：∵四边形ABCD是矩形， ∴AD∥BC，∠ABC＝90°，AD＝BC， ∵BE⊥AC于点F， ∴∠EAC＝∠ACB，∠ABC＝∠AFE＝90° ... ...