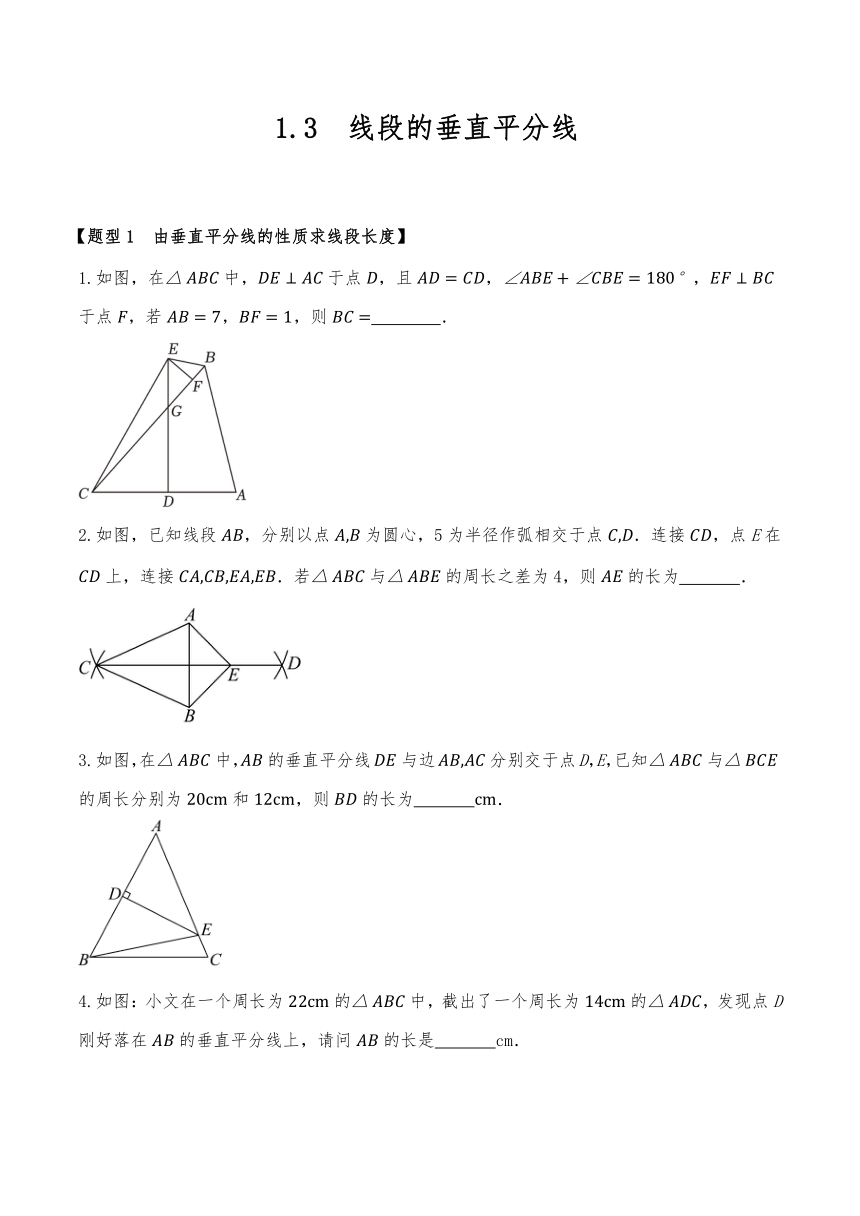
1.3 线段的垂直平分线 【题型1 由垂直平分线的性质求线段长度】 1.如图,在中,于点,且,,于点,若,,则 . 2.如图,已知线段,分别以点为圆心,5为半径作弧相交于点.连接,点E在上,连接.若与的周长之差为4,则的长为 . 3.如图,在中,的垂直平分线与边分别交于点D,E,已知与的周长分别为和,则的长为 . 4.如图:小文在一个周长为的中,截出了一个周长为的,发现点D刚好落在的垂直平分线上,请问的长是 cm. 【题型2 由垂直平分线的性质求周长】 1.如图,在中,,,,的垂直平分线交于点,交于点,则的周长为( ) A.18 B.14 C.17 D.19 2.如图,在中,,的垂直平分线交边于点,的垂直平分线交边于点,则的周长是( ) A. B.10 C.12 D. 3.如图,在中,.的周长为6,则的周长是 . 4.如图,在中,的垂直平分线分别与交于点D、E,的垂直平分线分别与交于点F、G,,,则的周长是 . 【题型3 由垂直平分线的性质求角度】 1.如图,,点O是,的垂直平分线,的交点,则的度数为( ) A.145° B.150° C.160° D.165° 2.如图,△ABC中,∠A=40°,AB的垂直平分线分别交AB,AC于点D,E,连接BE,则∠BEC的大小为( ) A.40° B.50° C.80° D.100° 3.在中,的垂直平分线分别交于点 D,E,若,则的度数为( ) A. B. C. D. 4.如图,在中,平分,平分,点是、的垂直平分线的交点,连接、,若,则的大小为( ) A. B. C. D. 【题型4 由垂直平分线的性质求最值】 1.如图,在中,,D为的中点,分别以点A、B为圆心,以适当的长为半径作弧,两弧分别交于E,F,M为直线上任意一点.若,面积为10,则长度的最小值为( ) A.4 B.5 C.6 D.7 2.如图,的周长为30,,作边的垂直平分线分别交,于点.连接,若点是直线上的一个动点,则周长的最小值为 . 3.如图,在中,,D为边的中点,点E、F分别是边、上的点.将沿直线翻折,使点A与点C重合.点P是直线上的任意一点,连接、.若,的面积为9.则周长的最小值为 . 4. 我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴.如图,直线是线段的垂直平分线,P是上任一点,连接.将线段沿直线对折,我们发现与完全重合,由此即有:线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等. 已知:如图,,垂足为点C,,点P是直线上任意一点. 求证: 分析图中有两个直角三角形和,只要证明这两个三角形全等,便可证得. (1)请结合以上分析、利用图1写出“线段垂直平分线的性质定理”完整的证明过程. (2)定理应用:如图2,在中,的垂直平分线交与点N,交于点M,连接,若,的周长是. ①求的长 ②点P是直线上一动点,在运动的过程中,的周长是否存在最小值?若存在,标出点P的位置,并求出此时的周长;若不存在,说明理由. 【题型5 由垂直平分线的性质探究角度之间的关系】 1.如图,在中,、分别在、上,,是中点,试比较与的大小: (提示:可添加辅助线) 2.如图,,,点在的垂直平分线上. (1)线段、、三者之间的长度有什么关系? (2)线段与有怎样的关系呢? 3.如图, 中,是的中点,过点的直线交于,交的平行线于点,,交于点,连接、. (1)求证:; (2)请你判断与的大小关系,并说明理由. 4.如图,中,于点D,于点E,与交于点F. (1)求证:; (2)若点E恰在线段的垂直平分线上,求证:. 【题型6 由垂直平分线的性质进行证明】 1.如图,在中,点D为边的中点,过点B作交的延长线于点E. (1)求证:. (2)若,求证: 2.如图,分别是的中点,,垂足为,垂足为.求证:. 3.如图,在四边形ABDC中,AD所在直线垂直平分线段BC,过点C作交AB于点F,延长AB,CD交于点E.求证: (1)CB平分; (2). 4.如图,在中,平分,于点,交于点,交于 ... ...
~~ 您好,已阅读到文档的结尾了 ~~