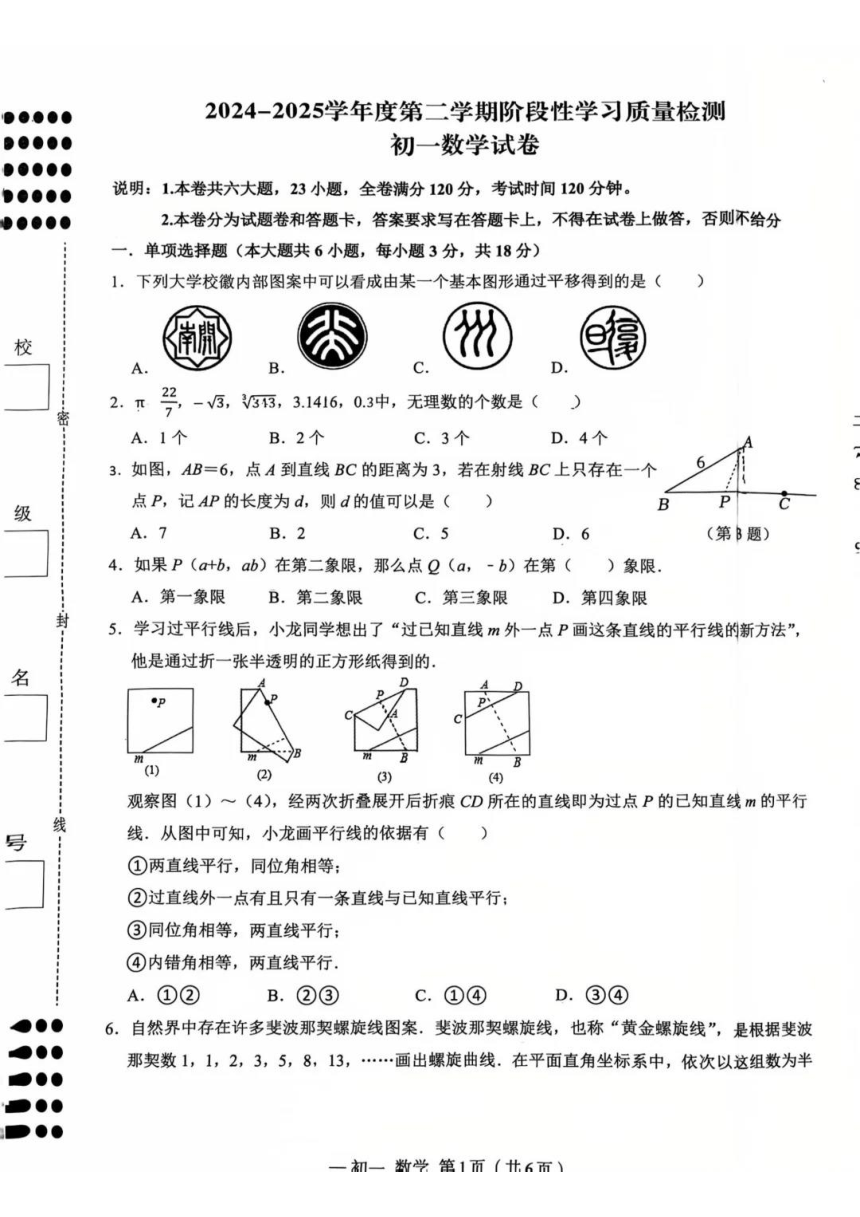
●0●●● 2024-2025学年度第二学期阶段性学习质量检测 ●0●00 初一数学试卷 ●00●0 D●●00 说明:1.本卷共六大题,23小题,全卷满分120分,考试时间120分钟。 0●●●● 2本卷分为试题卷和答题卡,答案要求写在答题卡上,不得在试卷上做答,否则不给分 单项选择题(本大题共6小题,每小题3分,共18分) 1.下列大学校徽内部图案中可以看成由某一个基本图形通过平移得到的是() 校 A D 2.π 22 -3,33,3.1416,0.3中,无理数的个数是( A.1个 B.2个 C.3个 D.4个 3.如图,AB=6,点A到直线BC的距离为3,若在射线BC上只存在一个 6 点P,记AP的长度为d,则d的值可以是() 级 B A.7 B.2 C.5 D.6 (第B题) 4.如果P(a+b,ab)在第二象限,那么点Q(a,-b)在第()象限. A.第一象限 B.第二象限 C.第三象限 D.第四象限 封 5.学行线后,小龙同学想出了“过已知直线m外一点P画这条直线的平行线的新方法”, 他是通过折一张半透明的正方形纸得到的, 名 (1) 2) (3) (4) 观察图(1)~(4),经两次折叠展开后折痕CD所在的直线即为过点P的已知直线m的平行 线 号 线.从图中可知,小龙画平行线的依据有() ①两直线平行,同位角相等: ②过直线外一点有且只有一条直线与已知直线平行: ③同位角相等,两直线平行: ④内错角相等,两直线平行. A.①② B.②③ C.①④ D.③④ ●0 6.自然界中存在许多斐波那契螺旋线图案,斐波那契螺旋线,也称“黄金螺旋线”,是根据斐波 ●● 那契数1,1,2,3,5,8,13,…画出螺旋曲线.在平面直角坐标系中,依次以这组数为半 ●●0 一却一数学第1而(t6而) 径作90°的圆弧P1P2,P2P3,P3P4,得到一组螺旋线,连接P1P2,P2P3,P3P4,,得到一 组螺旋线,如图所示.己知点P1,P2,P3的坐标分别为(-1,0),(0,1),(1,0),则点P 的坐标为() A.(6,1) B.(8,0) C.(8,2) D.(9,-2) 二.填空题(本大题共6小题,每小题3分,共18分) 7.把命题“相等的角是对顶角”改写成“如果…,那么…”的形式是 8.利用计算器,得V0.05≈0.2236,0.5≈0.7071,5≈2.236,50≈7.071,按此规律,可得V500 的值约为 9.将P点(m,m+4)向上平移2个单位到Q点,且点Q在x轴上,那么P点坐标为 10.如图,将一张长方形纸片沿EF折叠后,点C,D分别落在C,D的位置,若∠EFB=65°, 则∠AED'的度数为 ”, B C (第10题) (第12题) 行 11.已知点A(3a-6,a+4)、B(-3,2),且AB∥y轴,点P为直线AB上一点,且PA=4PB, 则点P的坐标为 12.如图,在△ABC中,∠BAC=45°,∠ACB是锐角,将△ABC沿着射线BC方向平移得到△ DEF(平移后点A,B,C的对应点分别是点D,E,F),连接CD,若在整个平移过程中,∠ ACD和∠CDE的度数之间存在2倍关系,则∠ACD= 三.解答题(本大题共5小题,每小题6分,共30分) 13.(1)计算:√-2)7--27+W3-2引+3: (2)解方程:9(x+1)2-169=0. 皮 长 一初一数学第2页(共6页)一 ... ...
~~ 您好,已阅读到文档的结尾了 ~~