第十九章矩形、菱形、正方形单元测试（一）（含答案）

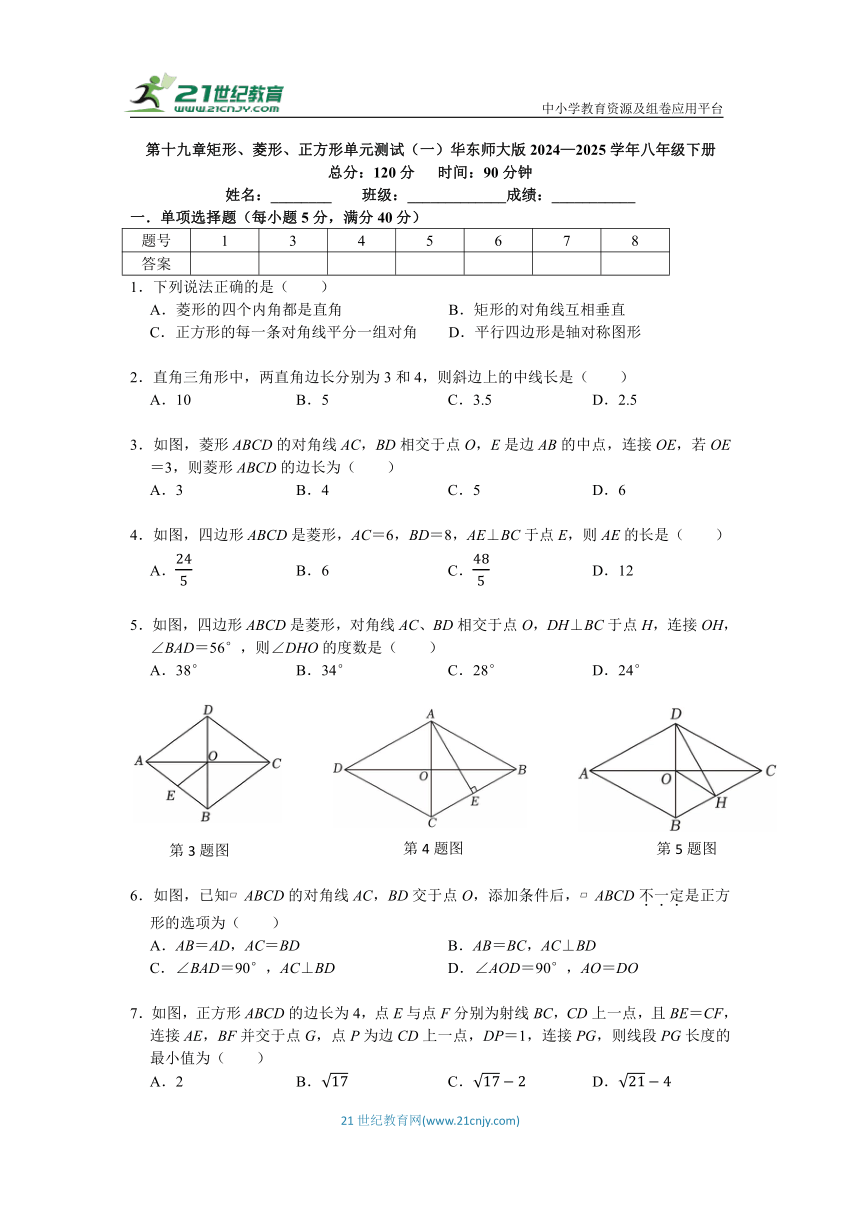
中小学教育资源及组卷应用平台 第十九章矩形、菱形、正方形单元测试（一）华东师大版2024—2025学年八年级下册 总分：120分 时间：90分钟 姓名：_____ 班级：_____成绩：_____ 一．单项选择题（每小题5分，满分40分） 题号 1 3 4 5 6 7 8 答案 1．下列说法正确的是（　　） A．菱形的四个内角都是直角 B．矩形的对角线互相垂直 C．正方形的每一条对角线平分一组对角 D．平行四边形是轴对称图形 2．直角三角形中，两直角边长分别为3和4，则斜边上的中线长是（　　） A．10 B．5 C．3.5 D．2.5 3．如图，菱形ABCD的对角线AC，BD相交于点O，E是边AB的中点，连接OE，若OE＝3，则菱形ABCD的边长为（　　） A．3 B．4 C．5 D．6 4．如图，四边形ABCD是菱形，AC＝6，BD＝8，AE⊥BC于点E，则AE的长是（　　） A． B．6 C． D．12 5．如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥BC于点H，连接OH，∠BAD＝56°，则∠DHO的度数是（　　） A．38° B．34° C．28° D．24° 6．如图，已知 ABCD的对角线AC，BD交于点O，添加条件后， ABCD不一定是正方形的选项为（　　） A．AB＝AD，AC＝BD B．AB＝BC，AC⊥BD C．∠BAD＝90°，AC⊥BD D．∠AOD＝90°，AO＝DO 7．如图，正方形ABCD的边长为4，点E与点F分别为射线BC，CD上一点，且BE＝CF，连接AE，BF并交于点G，点P为边CD上一点，DP＝1，连接PG，则线段PG长度的最小值为（　　） A．2 B． C． D． 8．如图，在正方形ABCD中，AB＝8，点F为边AB上的一点，连接CF交BD于点G，且CG＝2FG，点E是对角线BD上的一点，连接EF，CE．若EF⊥CE，则△BCE的面积为（　　） A．8 B．16 C．20 D．24 二．填空题（每小题5分，满分20分） 9.如图，菱形ABCD中，AB＝6，∠A＝120°，点M、N、P分别为线段AB、AD、BD上的任意一点，则PM+PN的最小值为　 ． 10.如图，矩形ABCD中，已知AB＝3，BC＝BE＝6，F为BE上一点，且，连接DE、CE、CF．以下说法中： ①BF＝2；②当点E在AD边上时，则∠DCE＝15°； ③当∠EBC＝60°时，则∠ADE＝30°；④DE+CF的最小值为5． 正确的有 　 　（填序号即可） 11.如图正方形ABCD中，E是BC边的中点，将△ABE沿AE对折至△AFE，延长EF交CD于G，连接CF，AG．下列结论：①AE∥FC； ②∠EAG＝45°，且BE+DG＝EG；③S△CEF＝S正方形ABCD； ④AD＝3DG，正确的是　 　（填序号）． 12.如图，在平面直角坐标系中，正方形ABCD顶点A的坐标为（0，2），B点在x轴上，对角线AC，BD交于点M，OM＝，则点C的坐标为　 　． 三．解答题（共8小题，总分60分，每题须有必要的文字说明和解答过程） 13．如图，△ABC中，AB＝AC，AD平分∠BAC，BE∥AD，AE⊥AD． （1）求证：四边形ADBE是矩形； （2）作EF⊥AB于F，若BC＝4，AD＝3，求EF的长． 14．如图，在四边形ABCD中，AD＝AB＝BC，AC⊥BD交于点O． （1）求证：四边形ABCD为菱形； （2）如图2，过四边形ABCD的顶点A作AE⊥BC于点E，交OB于点H，若AB＝AC＝6，求四边形OHEC的面积． 15．如图所示，在四边形ABCD中，对角线AC，BD相交于点O，AO＝CO＝10，BO＝DO，且AB＝12，BC＝16． （1）求证：四边形ABCD是矩形． （2）若∠ADF：∠FDC＝3：2，DF⊥AC于点E，求∠BDF的度数． 16．在正方形ABCD中，点F是边AB上一点，连接DF，点E为DF中点．连接BE、CE、AE． （1）求证：∠DAE＝∠ADE； （2）求证：△AEB≌△DEC； （3）当EB＝BC时，求∠AFD的度数． 17．如图①正方形ABCD中，点E是对角线AC上任意一点，连接DE，BE． （1）求证：DE＝BE； （2）当AE＝AB时，求∠BED的度数； （3）如图②，过点E作EF⊥DE交AB于点F，当BE＝BF时，若AB．求AF的长． 18．在菱形ABCD中，对角线AC、BD相交于点O，过点O直线EF分别交DA、BC的延长线于点E、F，连接BE、DF． （1）求证：△ ... ...