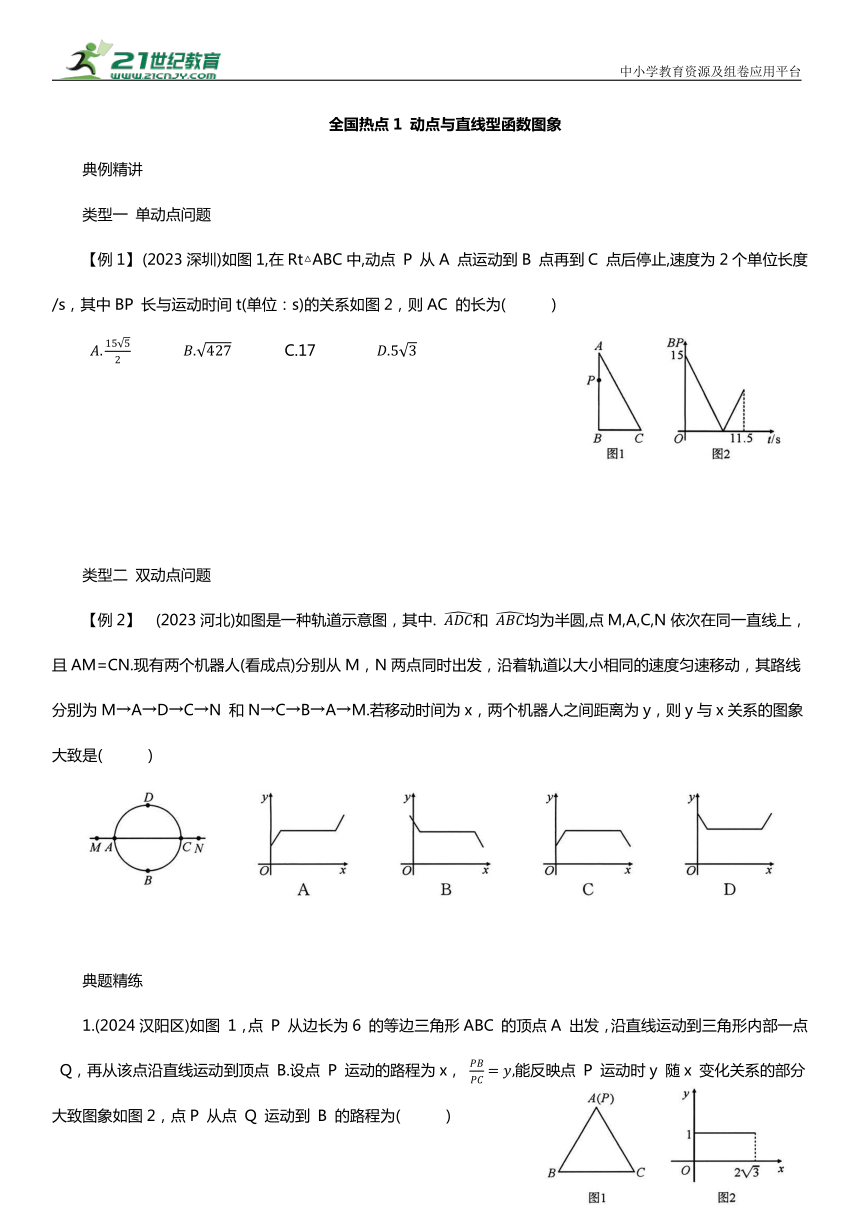
中小学教育资源及组卷应用平台 全国热点1 动点与直线型函数图象 典例精讲 类型一 单动点问题 【例1】 (2023深圳)如图1,在Rt△ABC中,动点 P 从A 点运动到B 点再到C 点后停止,速度为2个单位长度/s,其中BP 长与运动时间t(单位:s)的关系如图2,则AC 的长为( ) C.17 类型二 双动点问题 【例2】 (2023河北)如图是一种轨道示意图,其中. 和 均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N 和N→C→B→A→M.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( ) 典题精练 1.(2024汉阳区)如图 1,点 P 从边长为6 的等边三角形ABC 的顶点A 出发,沿直线运动到三角形内部一点 Q,再从该点沿直线运动到顶点 B.设点 P 运动的路程为x, 能反映点 P 运动时y 随x 变化关系的部分大致图象如图2,点P 从点 Q 运动到 B 的路程为( ) A.6 B.3 D. 2.如图,在正方形ABCD 中,点 P,Q从点A 出发,以1 cm/s的速度分别沿A—B—C 和A—D—C的路径匀速运动,同时到达点C 时停止运动.连接 PQ,设PQ的长为y,运动时间为x,则y(cm)与x(s)的函数图象如图所示.当x=2.5s 时,PQ 的长是 cm. 全国热点2 动点与曲线型函数图象 典例精讲 类型一 单动点问题 【例1】 (2024广州)如图1,点 P 从△ABC 的顶点A 出发,沿着A→B→C 的方向运动,到达点C 后停止.设点 P 的运动时间为x,AP 的长度为y,图2是y与x的关系图象,其中点 E 是曲线部分的最低点,则△ABC 的面积是 . 类型二 双动点问题 【例2】 (2024兰州)如图1,在菱形ABCD 中,∠ABC=60°,连接BD,点 M 从点B 出发沿BD 方向以 的速度运动至点 D,同时点 N 从点 B 出发沿BC 方向以1 cm/s的速度运动至点C,设运动时间为x(s),△BMN 的面积为y(cm ). y与x的函数图象如图2所示,则菱形ABCD 的边长为( ) C.4 cm D. 8cm 典题精练 1.(2023甘肃)如图1,正方形ABCD 的边长为4,E 为CD边的中点.动点 P 从点A 出发沿AB→BC 匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,线段 PE 的长为y,y与x的函数图象如图2所示,则点 M 的坐标为( ) A.(4,2 B.(4,4) C.(4,2 D.(4,5) 2.(2024武汉模拟)如图1,在△ABC 中,∠B=36°,动点P 从点A 出发,沿折线 A→B→C 匀速运动至点 C 停止.若点 P 的运动速度为1 cm/s,设点 P 的运动时间为t(s),AP 的长度为 y(cm),y 与 t 的函数图象如图 2 所示.当AP 恰好平分∠BAC 时t 的值为 . 全国热点1 动点与直线型函数图象 典例精讲 类型一 单动点问题 【例1】 (2023深圳)如图1,在Rt△ABC中,动点 P 从A 点运动到B 点再到C 点后停止,速度为2个单位长度/s,其中BP 长与运动时间t(单位:s)的关系如图2,则AC的长为( C ) C.17 解:由图象可知:t=0时,点P 与点A 重合,∴AB=15,∴点P 从点A运动到点B 所需的时间为15÷2=7.5(s),∴点 P 从点B 运动到点C 的时间为11.5-7.5=4(s),∴BC=2×4=8,在Rt△ABC中,由勾股定理可得AC=17.故选 C. 类型二 双动点问题 【例2】 (2023河北)如图是一种轨道示意图,其中 和 均为半圆,点M,A,C,N依次在同一直线上,且AM=CN.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为M→A→D→C→N 和N→C→B→A→M.若移动时间为x,两个机器人之间距离为y,则y与x关系的图象大致是( D ) 典题精练 1.(2024汉阳区)如图1,点 P 从边长为6 的等边三角形ABC 的顶点 A 出发,沿直线运动到三角形内部一点 Q,再从该点沿直线运动到顶点 B.设点 P 运动的路程为x, 能反映点 P 运动时y 随x变化关系的部分大致图象如图2,点P 从点Q 运动到B 的路程为( C ) A.6 B.3 D. 2.如图,在正方形ABCD 中,点 P,Q从点A 出发,以1cm/s的速度分别沿A--B-C 和A- ... ...
~~ 您好,已阅读到文档的结尾了 ~~

