2025年中考数学复习--板块二十四 圆(三)图形研究——解答题（含答案）

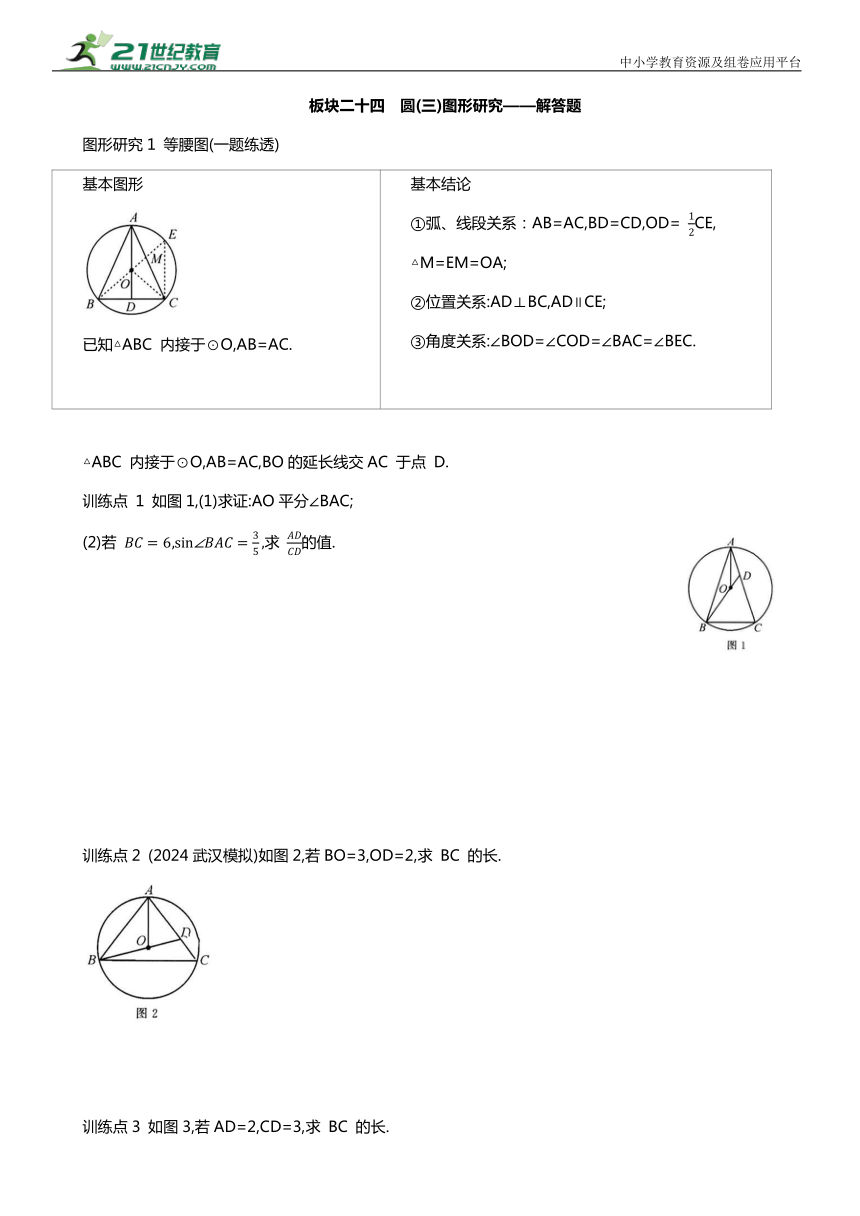
板块二十四 圆(三)图形研究———解答题 图形研究1 等腰图(一题练透) 基本图形 已知△ABC 内接于⊙O,AB=AC. 基本结论 ①弧、线段关系：AB=AC,BD=CD,OD= CE, △M=EM=OA; ②位置关系:AD⊥BC,AD∥CE; ③角度关系:∠BOD=∠COD=∠BAC=∠BEC. △ABC 内接于⊙O,AB=AC,BO的延长线交AC 于点 D. 训练点 1 如图1,(1)求证:AO平分∠BAC; (2)若 求 的值. 训练点2 (2024武汉模拟)如图2,若BO=3,OD=2,求 BC 的长. 训练点3 如图3,若AD=2,CD=3,求 BC 的长. 图形研究2 腰径图(一题练透) 基本图形:已知AB=AC,AB 是直径. 基本结论 ①三线合一:AD⊥BC,∠BAD=∠CAD,BD=CD; ②直径对直角:∠ADB=∠AEB=90°, BD=CD=DE; ③构中位线：(OD≌ AC. 在 中， ,以AB 为直径的⊙O 交BC 于点 D. 训练点1 如图1， 于点 F,交 BA 的延长线于点 E. (1)求证:DE 是⊙O 的切线; (2)若 求AF 的长. 训练点2 如图2,CA 的延长线交⊙O 于点E,过点 D 作. 于点H，连接DE 交线段OA于点 F.若A为EH 的中点，求 的值. 训练点3 如图3,过点 D 作AC 的垂线,垂足为 E.连接OE 交⊙O 于点 F,连接 DF,若 tan 求 cos∠DEF 的值. 图形研究3 切割图(一)(一题练透) 基本图形 条件:BC 是直径,AD 是切线. 结论:①∠CAD=∠B;②△ACD∽△BAD; ③AD =DC·DB. BC 是⊙O 的直径,D 为CB 延长线上一点,DA 切⊙O 于点A.训练点1 如图1，若 求⊙O 的半径. 训练点 2 (2024雅安)如图2,(1)若 求证： (2)若 于点H， 求AD 的长. 训练点3 如图3，P 是 的中点,AP 交BC 于点E. (1)求证: (2)若 求AE 的长. 图形研究5 割线图 基本图形 条件:AB=AC,EDA,ECB 是割线. 结论:∠ABD=∠E, △ABD∽△CED∽△AEB, △EBD∽△EAC,AB =AD·AE. 典例精讲 【例】 (2023江汉区)如图,AB 为⊙O 的直径,弦CD⊥AB,垂足为E,K 为 上一动点，AK,DC 的延长线相交于点 F,连接CK,KD. (1)求证:∠AKD=∠CKF; (2)若AB=10,CD=6,求 tan∠CKF 的值. 典题精练 1.如图,四边形ABCD 内接于⊙O,AB=AC,连接BD,延长AD,BC 交于点E. (1)求证:∠ABD=∠E; (2)若 求 CD 的长. 2.如图,点 A,B,C在半径为5的⊙O上,且. ,点 D 在劣弧AC上,连接AD 并 延长交BC 的延长线于点E. (1)若 求证:CE=AC; (2)若AD=6,求 DE 的长. 图形研究6 双切图(一题练透) 基本图形(课本101 页第6题) AC 是直径,PA,PB 是切线. 基本结论 ①PA=PB,∠1=∠2=∠3=∠CBD,∠DOB=∠APB; ②OP⊥AB,,AP=BF,AE=BE,OE⊥ BC; ③△BOD∽△APD,△BCD∽△ABD; ④△AOE∽△ACB∽△PAE∽△POA. AB 是⊙O的直径,BC,DC 为⊙O 的切线,切点分别为B,D,BA,CD 的延长线交于点E.训练点1 (2024 湖北改)如图1,连接OC,交⊙O于点F.若 求 的长. 训练点 2 如图2,连接AD,BD.若 ,求⊙O 的半径. 训练点 3 如图3,连接 DA,若 求线段 DE 的长. 图形研究7 多切图(一题练透) 基本图形条件:∠ACB=90°,⊙O 与BC,AC,AB 分别相切于点E,F,D. 结论:AD=AF,CE=CF,BE=BD, 四边形 OECF 是正方形. 在Rt△ABC 中,∠C=90°,⊙O 是△ABC 的内切圆,与三边 AC,BC,AB 分别相切于点E,F,G. 训练点1 如图1,若AC=3,BC=4. (1)求⊙O 的半径r; (2)求 tan∠OAG 的值. 训练点2 如图2,连接OA,OB,若BF=AC=3,⊙O的半径是1,求图中阴影部分的面积. 训练点3 (2024自贡)如图3,延长AC 到点M,使AM=AB,过点M 作MN⊥AB 于点N.求证:MN 是⊙O 的切线. 图形研究9 内心图(一题练透) 基本图形(课本124页第13 题) 条件:点 I 是△ABC 的内心. 结论:①BD=CD=ID; ②BD =DE·DA. 已知点 I 是 的内心，AI 的延长线与， 的外接圆⊙O交于点D. 训练点1 如图1,AD 与BC 交于点E,连接 BD,BI.若 ,求 AI 的长. 训练点2 如图2,AB 为⊙O 的直径,( 求 的值. 训练点 3 (2024巴中改)如图3,过点 D 作 ，交AC 的延长线于点 F.若 求AB 的长. 图形研究10 径切图 基本图形 条件:AB 是⊙O 的直径,AC 是⊙O 的切 ... ...