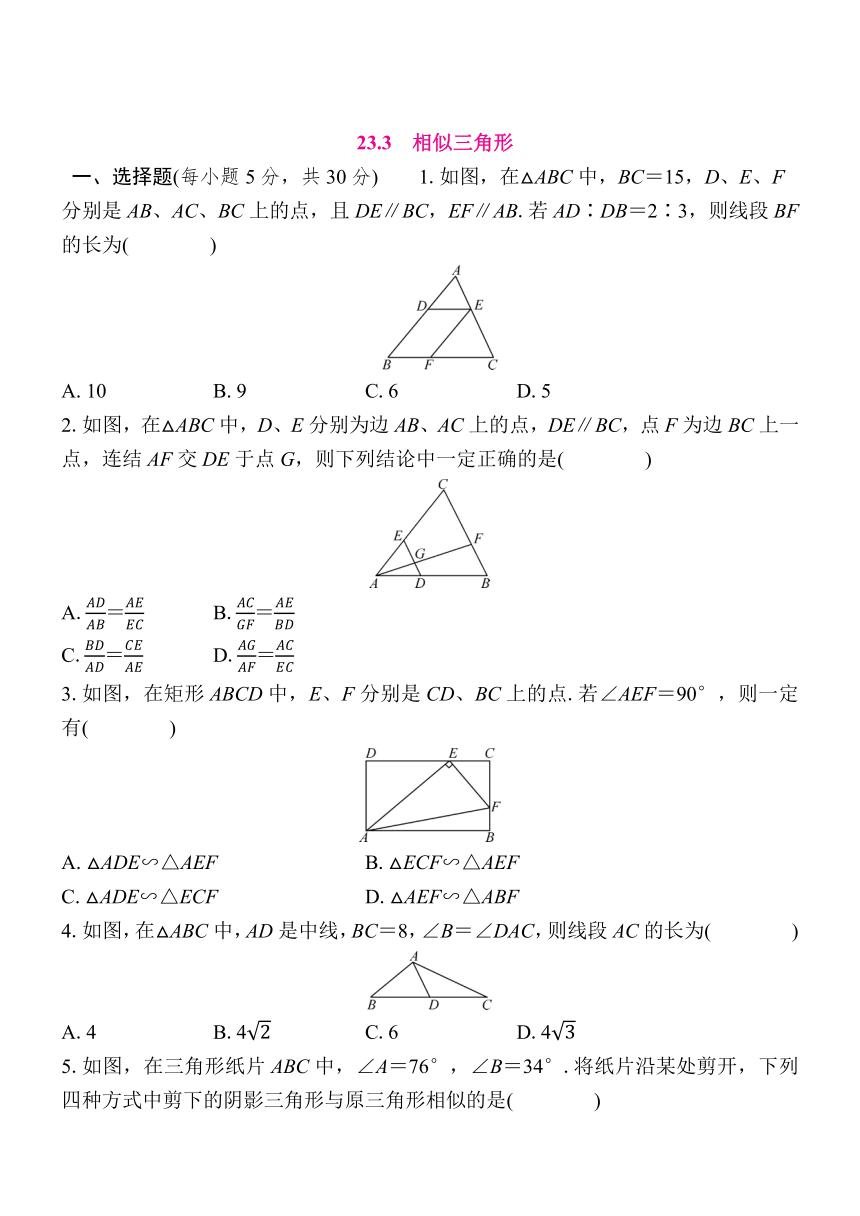
23.3 相似三角形 一、选择题(每小题5分,共30分) 1.如图,在△ABC中,BC=15,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB.若AD∶DB=2∶3,则线段BF的长为( ) A.10 B.9 C.6 D.5 2.如图,在△ABC中,D、E分别为边AB、AC上的点,DE∥BC,点F为边BC上一点,连结AF交DE于点G,则下列结论中一定正确的是( ) A.= B.= C.= D.= 3.如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有( ) A.△ADE∽△AEF B.△ECF∽△AEF C.△ADE∽△ECF D.△AEF∽△ABF 4.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( ) A.4 B.4 C.6 D.4 5.如图,在三角形纸片ABC中,∠A=76°,∠B=34°.将纸片沿某处剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是( ) A.①② B.②④ C.①③ D.③④ 6.如图,在正方形ABCD中,AB=2,N为边AD上一点,连结BN,过点A作AP⊥BN于点P,点M为边AB上一点,且∠PMA=∠PCB,连结CM.下列结论中正确的个数为( ) ①△PAM∽△PBC;②PM⊥PC;③∠MPB=∠MCB;④若点N为AD中点,则S△PCN=6;⑤AN=AM. A.5 B.4 C.3 D.2 二、填空题(每小题5分,共30分) 7.在比例尺为1∶10 000 000的地图上,量得甲、乙两个城市之间的距离是8cm,那么甲、乙两个城市之间的实际距离应为 km. 8.若下图中两个三角形相似,则x= . 9.如图,已知∠A=∠D,不添加辅助线和字母,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件) 10.如图,在平行四边形ABCD中,F是对角线BD上的一点,连结AF并延长,交BC于点E.已知BF∶FD=2∶3,BC=12cm,则CE= cm. 11.如图,在△ABC中,AB=8,AC=6,点D在AC上,且AD=2.如果要在AB上找一点E,使△ADE与△ABC相似,则AE的长为 . 12.[2024秋·临汾期中]如图,在△ABC中,点D在边AC上,AD∶DC=1∶2,O是BD的中点,连结AO并延长,交BC于点E.若BE=3,则BC的长为 . 三、解答题(共40分) 13.(8分)如图,在等腰三角形ABC中,AB=AC,点E、F在线段BC上,点Q在线段AB上,且CF=BE,AE2=AQ·AB.求证: (1)AE=AF; (2)△CAF∽△BFQ. 14.(8分)[2024秋·山西长治市壶关县期中]如图,在矩形ABCD中,AE⊥BD于点E,连结CE,过点E作EF⊥EC交AD于点F. (1)求证:AE·AB=DE·AF; (2)若AB=1,BC=2,求FD的长. 15.(12分)[2024·内江二模]如图,在△ABC中,点D、E、F分别在边AC、BD、BC上.从下列条件中选择两个作为本题的条件.①AB2=AD·AC;②∠BAE=∠CAF;③=. (1)求证:△ABE∽△ACF; (2)连结EF,如果BF=CF,求证:EF∥AC. 16.(12分)阅读与思考. 射影定理:如图1,在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有如下结论:①AD2=BD·DC;②AB2=BD·BC;③AC2=CD·BC. 下面是该定理的证明过程(部分): ∵AD是斜边BC上的高, ∴∠ADB=∠ADC=90°. ∵∠B+∠BAD=90°,∠B+∠C=90°, ∴∠BAD=∠C, ∴△ABD∽△CAD(依据), ∴=,即AD2=BD·DC. (1)材料中的依据是指 ; (2)选择②或③其中一个加以证明; (3)如图2,在正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE于点F,连结OF,求证:BO·BD=BF·BE; (4)在图2中,若DE=2CE,OF的长为,则正方形ABCD的边长为 . 参考答案 1.C 2.C 3.C 4.B 5.C 6.B 7.800 8.2 9.AB∥DE(答 ... ...
~~ 您好,已阅读到文档的结尾了 ~~