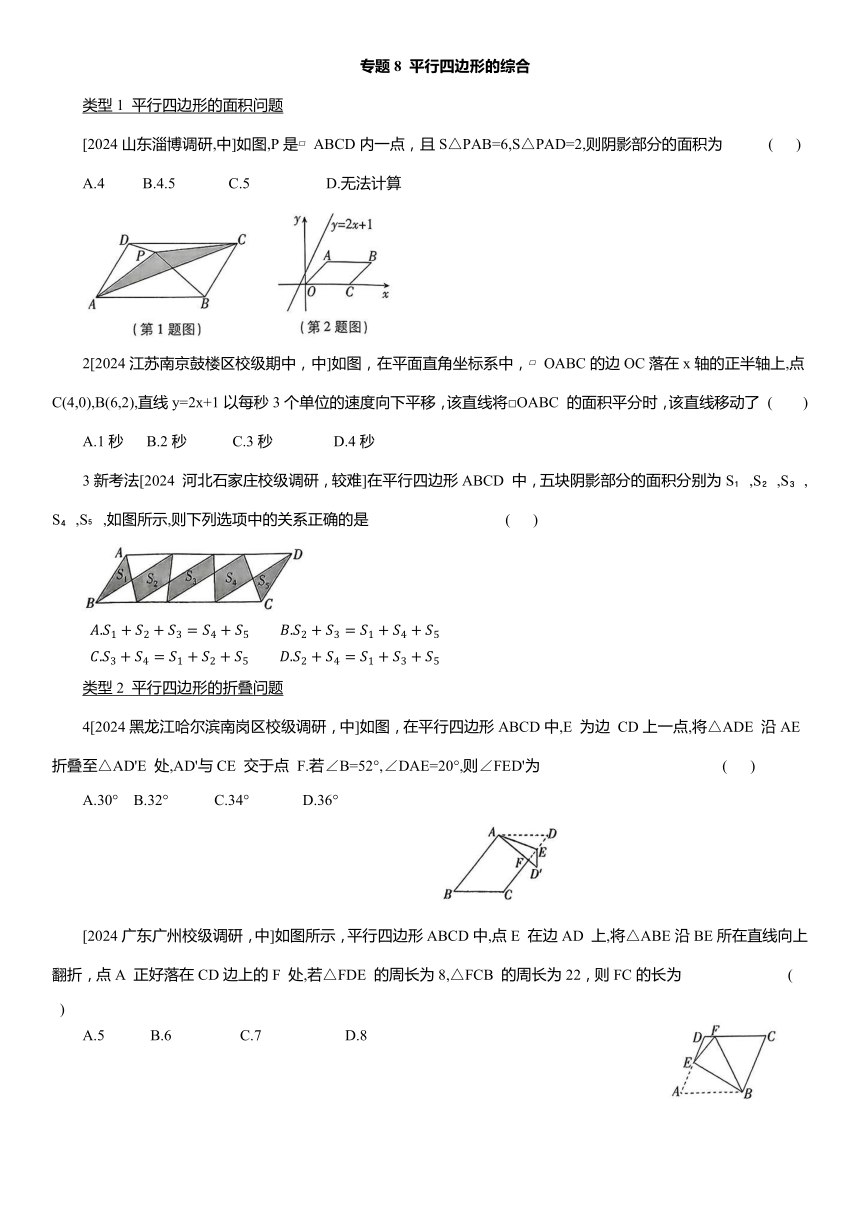
专题8 平行四边形的综合 类型1 平行四边形的面积问题 [2024山东淄博调研,中]如图,P是 ABCD内一点,且S△PAB=6,S△PAD=2,则阴影部分的面积为 ( ) A.4 B.4.5 C.5 D.无法计算 2[2024江苏南京鼓楼区校级期中,中]如图,在平面直角坐标系中, OABC的边OC落在x轴的正半轴上,点C(4,0),B(6,2),直线y=2x+1以每秒3个单位的速度向下平移,该直线将□OABC 的面积平分时,该直线移动了 ( ) A.1秒 B.2秒 C.3秒 D.4秒 3新考法[2024 河北石家庄校级调研,较难]在平行四边形ABCD 中,五块阴影部分的面积分别为S ,S ,S ,S ,S ,如图所示,则下列选项中的关系正确的是 ( ) 类型2 平行四边形的折叠问题 4[2024黑龙江哈尔滨南岗区校级调研,中]如图,在平行四边形ABCD中,E 为边 CD上一点,将△ADE 沿AE 折叠至△AD'E 处,AD'与CE 交于点 F.若∠B=52°,∠DAE=20°,则∠FED'为 ( ) A.30° B.32° C.34° D.36° [2024广东广州校级调研,中]如图所示,平行四边形ABCD中,点E 在边AD 上,将△ABE沿BE所在直线向上翻折,点A 正好落在CD边上的F 处,若△FDE 的周长为8,△FCB 的周长为22,则FC的长为 ( ) A.5 B.6 C.7 D.8 6[2024 山东济南校级调研,较难]如图,,S□ABCD=24,点E 为AB 的中点,点 F 为 BC 上的一个动点,将△BEF沿EF 折叠,点 B 的对应点为点 G,连接GD,GC,若AB=4,则△GDC面积的最小值为 7[2024河北唐山校级期中,中]如图,将 ABCD沿过点A 的直线折叠,使点 D 落到AB 边上的点 D'处,折痕交 CD 边于点 E,连接BE. (1)求证:四边形BCED'是平行四边形; (2)若BE平分∠ABC,求证: 8[2024四川成都期中,中]如图,将平行四边形ABCD 折叠,使得点 C 落在点A 处,点 D 落在点D'处,折痕为EF,连接CE. (1)求证:四边形AFCE 是平行四边形; (2)若AB=4,BC=6,∠B=60°,求平行四边形AFCE 的面积. 类型3 平行四边形的动点问题 [2024江苏连云港校级调研,中]如图,直线AB与x轴,y轴分别交于点A(3,0),B(0,6),另有两点C(-1,4),D(-3,4),若点P是直线AB上的动点,点Q为y轴上的动点,要使以Q,P,C,D为顶点的四边形是平行四边形,且线段 CD 为平行四边形的一边,则满足条件的 P 点坐标为 10[2024江苏南京鼓楼区期末,较难]如图,在 ABCD中,点 D 是定点,点A,C 分别是直线l 和l 上两动点,且l ∥l ,点D到直线l 和l 的距离分别是1 和4,则对角线 BD 长度的最小值是 . 11[2024山东济南校级调研,中]如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15 cm,点P 自点A 向点 D 以1 cm/s的速度运动,到D 点即停止.点 Q 自点 C 向点 B 以2cm/s的速度运动,到B 点即停止,点P,Q同时出发,设运动时间为 ts. (1)用含 t的代数式表示各线段长度. AP= ;DP= ;BQ= ;CQ= . (2)当 t 为何值时,四边形 APQB 是平行四边形 (3)当 t 为何值时,四边形 PDCQ 是平行四边形 12[2024广东河源源城区期末,较难]如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从D 点出发,以每秒1个单位的速度沿DA 向点A 匀速移动,点F 从点 C 出发,以每秒3个单位的速度沿 C→B→C 做匀速移动,两个点同时出发,当有一个点到达终点时,另一点也随之停止运动.点G为BD上的一点,连接EG,FG,设移动时间为t秒,BG的长度为y. (1)求证:AD∥BC; (2)在移动过程中,小明发现有△DEG 与△BFG全等的情况出现,请你探究这样的情况会出现几次,并分别求出此时的移动时间t和BG的长度y. 专题8 平行四边形的综合 刷难关 1. A 【解析】∵ 故选 A. 2. B 【解析】连接AC,BO 交于点 D.当平移后的直线经过D 点时,该直线可将 OABC 的面积平分.∵四边形 AOCB 是平行四边形,∴BD=OD.∵点B(6,2),O(0,0),∴D(3,1).设过点 D 的直线与x轴交于点 E,直线DE 的表达式为y= kx+b.∵直线DE 由直线y=2x+1 平移得到,∴k=2.∵ 直线 DE 过D(3,1),∴直线 DE 的表达式为 y=2x-5,∴直 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

