人教版（2024）数学七年级下册9.1.2用坐标描述简单几何图形 教案

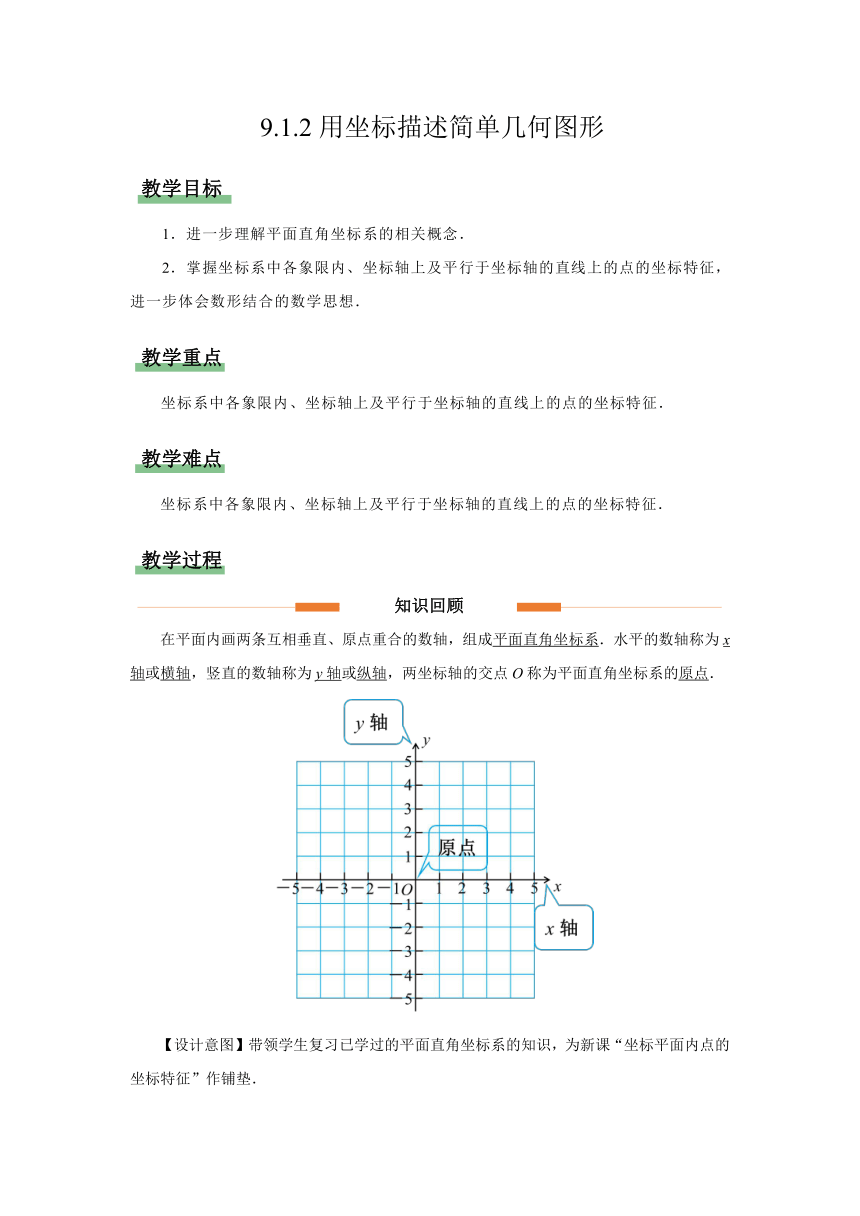
9.1.2用坐标描述简单几何图形 　　1．进一步理解平面直角坐标系的相关概念． 　　2．掌握坐标系中各象限内、坐标轴上及平行于坐标轴的直线上的点的坐标特征，进一步体会数形结合的数学思想． 　　坐标系中各象限内、坐标轴上及平行于坐标轴的直线上的点的坐标特征． 　　坐标系中各象限内、坐标轴上及平行于坐标轴的直线上的点的坐标特征． 知识回顾 　　在平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系．水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点O称为平面直角坐标系的原点． 　　【设计意图】带领学生复习已学过的平面直角坐标系的知识，为新课“坐标平面内点的坐标特征”作铺垫． 新知探究 一、探究学习 　　【新知】建立平面直角坐标系以后，坐标平面就被两条坐标轴分成了Ⅰ，Ⅱ，Ⅲ，Ⅳ四个部分，每个部分称为象限，它们分别叫作第一象限、第二象限、第三象限和第四象限．坐标轴上的点不属于任何象限． 　　【问题】（1）已知平面直角坐标系，写出图中点A，B，C，D的坐标． 　　【师生活动】教师提出问题，学生思考并回答． 　　图中点A，B，C，D的坐标分别为A(5，5)，B(3，－2)，C(－4，2)，D(－2，－3)． 　　教师追问：观察一下，各象限的点的坐标分别有什么特点？ 　　学生小组交流并派一名代表回答，教师总结． 点的位置 横坐标的符号 纵坐标的符号 第一象限 ＋ ＋ 第二象限 － ＋ 第三象限 － － 第四象限 ＋ － 　　【问题】（2）在平面直角坐标系中，点E，F，G，H的坐标分别是什么？ 　　【师生活动】教师提出问题，学生思考并回答． 　　点E，F，G，H的坐标分别是E(4，0)，F(－1，0)，G(0，3)，H(0，－2)． 　　教师追问：观察一下，坐标轴上的点的坐标分别有什么特点？ 　　学生小组交流并派一名代表回答，教师总结． 　　x轴上的点可表示为(x，0)； 　　y轴上的点可表示为(0，y)． 点的位置 横坐标的特点 纵坐标的特点 x轴 正半轴 ＋ 0 负半轴 － 0 y轴 正半轴 0 ＋ 负半轴 0 － 　　【设计意图】利用数形结合的方法，引导学生分析、解决问题，从而得出各象限内和坐标轴上的点的坐标特点． 二、典例分析 　　【例1】在平面直角坐标系中，点P(－2，－3)所在的象限是（　　）． 　　A．第一象限 B．第二象限 　　C．第三象限 D．第四象限 　　【师生活动】教师提出问题，学生思考并回答． 　　∵－2＜0，－3＜0， 　　∴点P(－2，－3)所在的象限是第三象限． 　　【答案】C 　　【例2】在平面直角坐标系中，点A(x，y)的坐标满足以下条件： 　　（1）若xy＞0，则点A在第_____象限； 　　（2）若xy＜0，则点A在第_____象限； 　　（3）若xy＝0，则点A在_____上． 　　【师生活动】教师提出问题，学生分小组交流并回答． 　　（1）若xy＞0，则x，y同正或者同负，所以点A在第一或三象限． 　　（2）若xy＜0，则x，y一正一负，所以点A在第二或四象限． 　　（3）若xy＝0，则x，y中至少有一个为0，所以点A在坐标轴上． 　　【答案】一或三　　二或四　　坐标轴 　　【例3】已知点P(2m－4，m＋1)，请根据以下条件求出点P的坐标． 　　（1）点P在x轴上； 　　（2）点P在y轴上； 　　（3）点P的横坐标比纵坐标大3． 　　【师生活动】教师提出问题，学生分小组交流并回答，教师板书． 　　【答案】解：（1）∵点P在x轴上，∴m＋1＝0，解得m＝－1． 把m＝－1代入横坐标，得2m－4＝－6． ∴点P的坐标为(－6，0)． 　　（2）∵点P在y轴上，∴2m－4＝0，解得m＝2． 　　把m＝2代入纵坐标，得m＋1＝3． 　　∴点P的坐标为(0，3)． 　　（3）由题意，得2m－4＝m＋1＋3，解得m＝8． 　　把m＝8分别代入横、纵坐标，得2m－4＝12，m＋1＝9． 　　点P的坐标为P(12，9)． 　　【设计意图】通过 ... ...