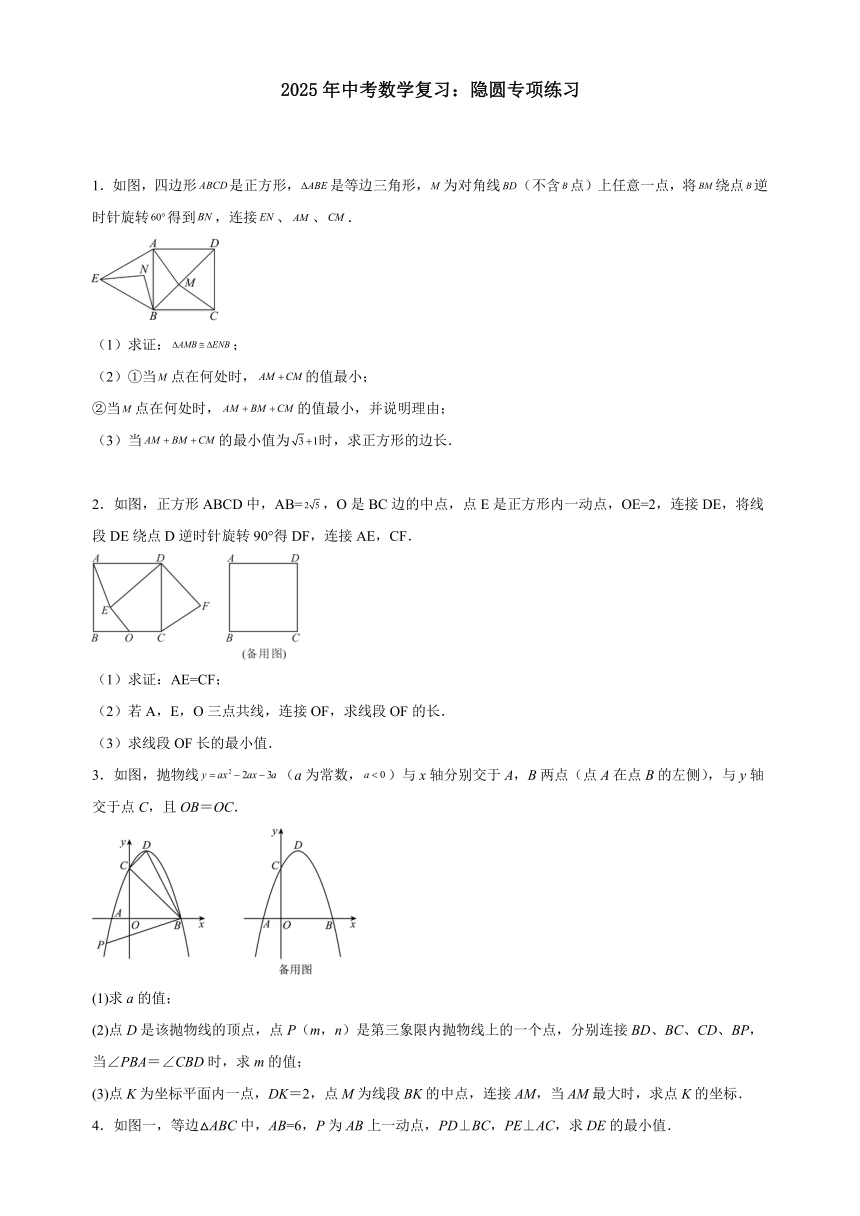
2025年中考数学复习：隐圆专项练习（含解析）

2025年中考数学复习：隐圆专项练习 1．如图，四边形是正方形，是等边三角形，为对角线（不含点）上任意一点，将绕点逆时针旋转得到，连接、、． （1）求证：； （2）①当点在何处时，的值最小； ②当点在何处时，的值最小，并说明理由； （3）当的最小值为时，求正方形的边长． 2．如图，正方形ABCD中，AB=，O是BC边的中点，点E是正方形内一动点，OE=2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE，CF． （1）求证：AE=CF； （2）若A，E，O三点共线，连接OF，求线段OF的长． （3）求线段OF长的最小值． 3．如图，抛物线（a为常数，）与x轴分别交于A，B两点（点A在点B的左侧），与y轴交于点C，且OB＝OC． (1)求a的值； (2)点D是该抛物线的顶点，点P（m，n）是第三象限内抛物线上的一个点，分别连接BD、BC、CD、BP，当∠PBA＝∠CBD时，求m的值； (3)点K为坐标平面内一点，DK＝2，点M为线段BK的中点，连接AM，当AM最大时，求点K的坐标． 4．如图一，等边△ABC中，AB=6，P为AB上一动点，PD⊥BC，PE⊥AC，求DE的最小值． 5．问题发现： （1）如图①，点A和点B均在⊙O上，且∠AOB＝90°，点P和点Q均在射线AM上，若∠APB＝45°，则点P与⊙O的位置关系是 ；若∠AQB＜45°，则点Q与⊙O的位置关系是 ． 问题解决： 如图②、图③所示，四边形ABCD中，AB⊥BC，AD⊥DC，∠DAB＝135°，且AB＝1，AD＝2，点P是BC边上任意一点． （2）当∠APD＝45°时，求BP的长度． （3）是否存在点P，使得∠APD最大？若存在，请说明理由，并求出BP的长度；若不存在，也请说明理由． 6．如图，在矩形ABCD中，AB＝6，AD＝8，点E，F分别是边CD，BC上的动点，且∠AFE＝90° （1）证明：△ABF∽△FCE； （2）当DE取何值时，∠AED最大． 7．如图，在等边中，点在边上，点为延长线上一点，连接，过点作交延长线于点． （1）如图1，若，，，求的长； （2）如图2，若，点在的垂直平分线上，点在边上，连接交于点，且，求证：； （3）如图3，若，，，点、、分别是三边上的动点，当周长取得最小值时，取线段的中点，点为平面内一点，且，连接、，请直接写出的最大值． 8．如图，在正方形中，点E在直线右侧，且，以为边作正方形，射线与边交于点M，连接、． (1)如图1，求证：； (2)若正方形的边长为4， ①如图2，当G、C、M三点共线时，设与交于点N，求的值； ②如图3，取中点P，连接，求长度的最大值． 9．如图1，与都是等边三角形，边长分别为4和，连接为高，连接，N为的中点． (1)求证：； (2)将绕点A旋转，当点E在上时，如图2，与交于点G，连接，求线段的长； (3)连接，在绕点A旋转过程中，求的最大值． 10．如图，等边三角形ABC内接于半径长为2的⊙O，点P在圆弧AB上以2倍速度从B向A运动，点Q在圆弧BC上以1倍速度从C向B运动，当点P，O，Q三点处于同一条直线时，停止运动． (1)求点Q的运动总长度； (2)若M为弦PB的中点，求运动过程中CM的最大值． 11．在平面直角坐标系中，二次函数的图像过点和点，与x轴交于点A、B（点A在点B的左边），且点D与点G关于坐标原点对称． (1)求该二次函数解析式，并判断点G是否在此函数的图像上，并说明理由； (2)若点P为此抛物线上一点，它关于x轴，y轴的对称点分别为M，N，问是否存在这样的P点使得M，N恰好都在直线DG上？如存在，求出点P的坐标，如不存在，并说明理由； (3)若第四象限有一动点E，满足，过E作轴于点F，设F坐标为，，的内心为I，连接CI，直接写出CI的最小值． 12．如图，在中，，，点D是延长线上一点，点E在线段上，于点F，交于点G． (1)如图1．若，．求的度数：（用含的代数式表示）： (2)如图2，若，证明：； (3)如图3，若．H为的中点，，当的面积最大时，请直接写出此时的值． 13．如图，四边形和均为正方形，将 ... ...