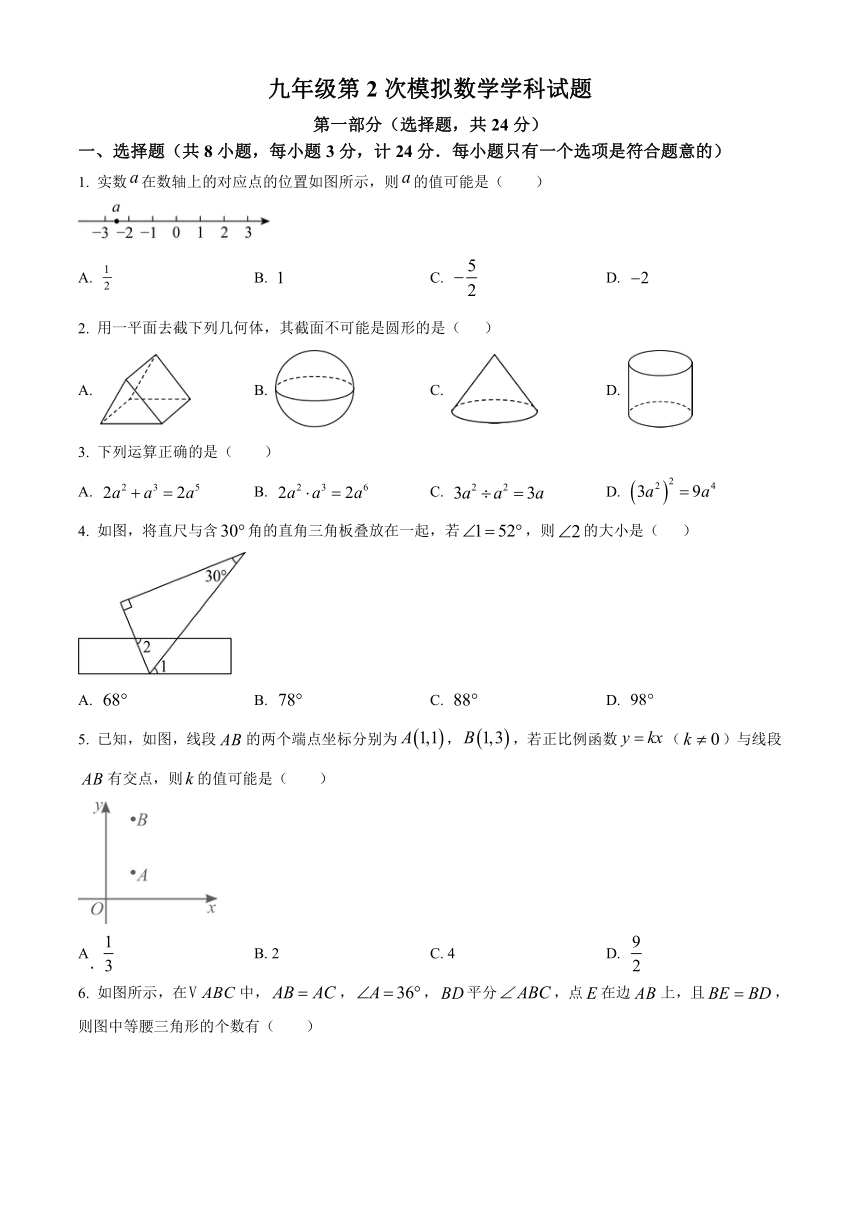
九年级第2次模拟数学学科试题 第一部分(选择题,共24分) 一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的) 1. 实数在数轴上的对应点的位置如图所示,则的值可能是( ) A. B. C. D. 2. 用一平面去截下列几何体,其截面不可能是圆形的是( ) A. B. C. D. 3. 下列运算正确的是( ) A. B. C. D. 4. 如图,将直尺与含角的直角三角板叠放在一起,若,则的大小是( ) A. B. C. D. 5. 已知,如图,线段的两个端点坐标分别为,,若正比例函数()与线段有交点,则的值可能是( ) A B. 2 C. 4 D. 6. 如图所示,在中,,,平分,点在边上,且,则图中等腰三角形的个数有( ) A. 3 B. 4 C. 5 D. 6 7. 如图,四边形是的内接四边形,,则的度数为( ) A. B. C. D. 8. 已知二次函数,当时,,则的值为( ) A. B. 3 C. 4 D. 第二部分(非选择题,共96分) 二、填空题(共5小题,每小题3分,计15分) 9. 比较大小:_____(填“”“”或“”). 10. 如图,点O是正八边形中心,连接,若,则点O到的距离为_____. 11. 如图,在菱形中,点是对角线上一点,连接,若,且, ,则的长为_____. 12. 如图,在平面直角坐标系中,矩形的顶点、在轴上,且面积为8,点在边上,,若点、在同一个反比例函数图象上,则该反比例函数的表达式为_____. 13. 如图,已知在中,,,,,点为射线上的动点,则的最大值为_____. 三、解答题(共13小题,计81分,解答应写出过程) 14. 计算:. 15. 解不等式,把解集在数轴上表示出来,并求出它的正整数解. 16. 解分式方程:. 17. 如图,点在直线外,点到直线的距离为4.请利用尺规作图法,作等腰,使、在直线上,且(作一个满足条件的三角形即可,不写作法,保留作图痕迹). 18. 如图,点、、在同一条直线上,,,.求证:. 19. 如图是某月的日历,小明说:他用一个平行四边形框,框出6个数字,其中最小数与最大数的积是 144,请求出最小数与最大数分别是多少. 20. 据统计,全国5棵树龄在5000年以上的古树名木均在陕西省境内,分别为延安市的“黄帝手植柏”(A)、“老君柏”()、“保生柏”(),渭南市的“仓颉手植柏”()和商洛市的“洛南古柏”().小伟和小峰想在周末去参观这些古树名木,并各自选择其中一棵制作宣传手抄报.他们制作了如图所示五等分的转盘;转动转盘,转盘停止后,指针所指的树木作为制作手抄报的素材(当指针指在分界线上时重转) (1)小伟转动转盘一次,转盘停止转动后,指针所指扇形中的树木是“老君柏”()的概率为_____. (2)两人各转动转盘一次,请用列表法或画树状图法,求小伟和小峰选择树木都位于延安市的概率. 21. 周末,小英与小淇同学逛公园时注意到一棵树,她们打算利用所学知识测量树高,为此找来了平面镜、直木棍、皮尺等工具.如图,小英先将平面镜(厚度不计)平放在水平地面的点D处,小淇站在点B处,通过平面镜从点A观察到树的顶端点M,随后小英在点D处竖直放置一根木棍,小淇从点A观察到术棍顶端点C与树的底端点N在同一直线上.已知,图中所有点均在同一平面内,求树的高.(光的反射角等于入射角) 22. 2023年2月6日土耳其发生7.8级地震,牵动世界各国人民的心!为进一步宣传防震减灾科普知识,增强学生应急避险和自救互救能力,某校组织全校学生进行“防震减灾知识测试”,现随机抽取部分学生的测试成绩(单位:分)整理成,,,四个等级,绘制成如下频数分布表和扇形统计图: 被抽取学生的测试成绩的频数表 等级 成绩/分 频数/人 各组总分/分 10 650 1050 21 1785 5 455 根据以上信息,解答下列问题: (1)填空:_____,_____; (2)此次被抽取学生的测试成绩的中位数落在_____等级,求此次被抽取学生的测试成绩 ... ...
~~ 您好,已阅读到文档的结尾了 ~~