18.2.3 正方形 分层练习(含答案)2024-2025学年人教版八年级数学下册

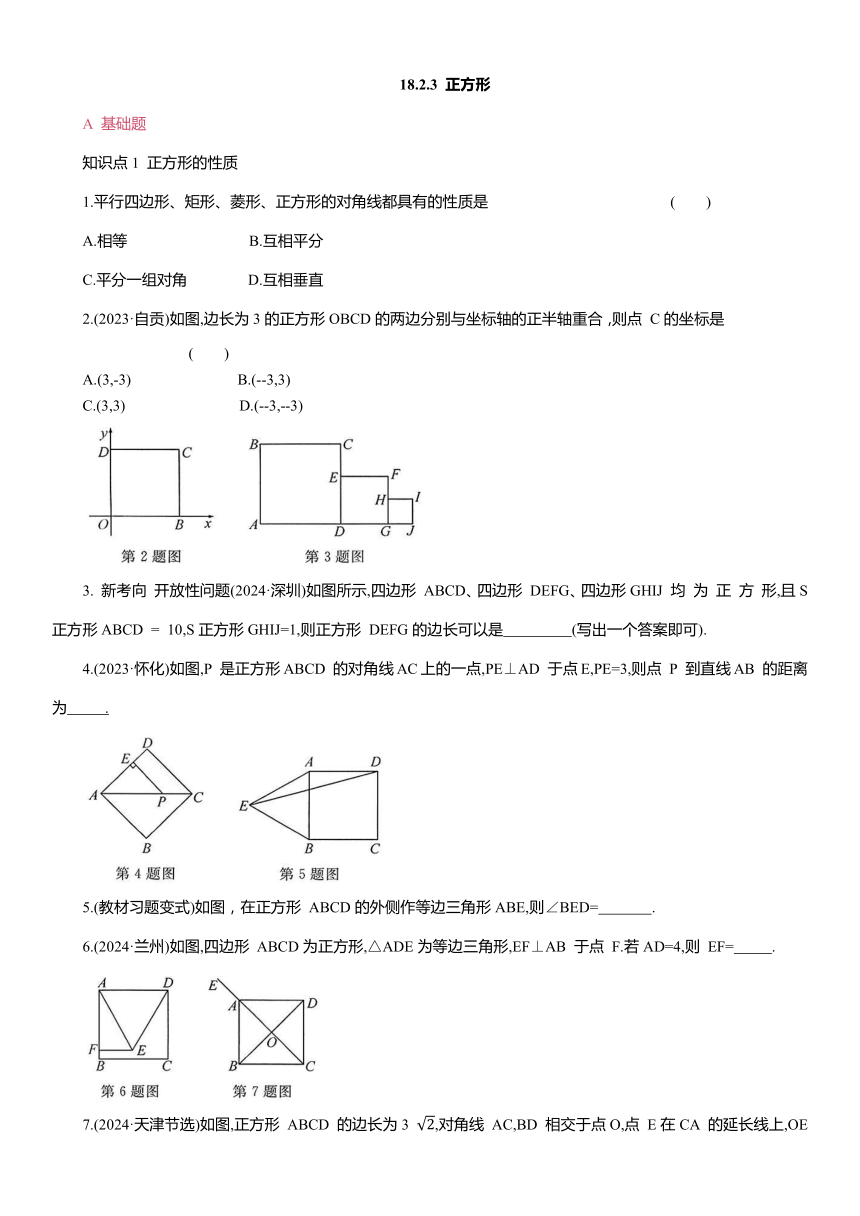
18.2.3 正方形 A 基础题 知识点1 正方形的性质 1.平行四边形、矩形、菱形、正方形的对角线都具有的性质是 ( ) A.相等 B.互相平分 C.平分一组对角 D.互相垂直 2.(2023·自贡)如图,边长为3的正方形OBCD的两边分别与坐标轴的正半轴重合，则点 C的坐标是 ( ) A.(3,-3) B.(--3,3) C.(3,3) D.(--3,--3) 3. 新考向 开放性问题(2024·深圳)如图所示,四边形 ABCD、四边形 DEFG、四边形GHIJ 均 为 正 方 形,且S正方形ABCD = 10,S正方形GHIJ=1,则正方形 DEFG的边长可以是 (写出一个答案即可). 4.(2023·怀化)如图,P 是正方形ABCD 的对角线AC上的一点,PE⊥AD 于点E,PE=3,则点 P 到直线AB 的距离为 . 5.(教材习题变式)如图，在正方形 ABCD的外侧作等边三角形ABE,则∠BED= . 6.(2024·兰州)如图,四边形 ABCD为正方形,△ADE为等边三角形,EF⊥AB 于点 F.若AD=4,则 EF= . 7.(2024·天津节选)如图,正方形 ABCD 的边长为3 ,对角线 AC,BD 相交于点O,点 E在CA 的延长线上,OE=5,则线段 AE 的长为 . 8.如图,在正方形 ABCD 中,E 为边 CD 上一点,F为 BC 延长线上一点,且CE=CF.求证:∠EBC=∠FDC. 知识点2 正方形的判定 9.下列说法中，正确的是 ( ) A.四边相等的四边形是正方形 B.四角相等的四边形是正方形 C.对角线互相垂直的平行四边形是正方形 D.对角线互相垂直平分且相等的四边形是正方形 10.新考向 开放性问题 (2024·黑龙江)如图,在菱形 ABCD 中,对角线AC,BD相交于点 O,请添加一个条件： ，使得菱形 ABCD为正方形. 11.(教材习题变式)如图，正方形ABCD的对角线AC,BD相交于点O,过点C作CE∥BD,过点 D作DE∥AC,CE,DE相交于点E.求证：四边形OCED是正方形. B 中档题 12.(教材习题变式)如图，已知正方形ABCD的两条对角线相交于点O，那么图中等腰直角三角形有 ( ) A.4个 B.6个 C.8个 D.10个 13.(2024·吉林)如图,正方形ABCD 的对角线AC,BD 相交于点O,E 是OA 的中点,F 是OD 上一点,连接EF.若∠FEO=45°,则 的值为 . 14.(2024·福建)如图,正方形 ABCD 的面积为4,E,F,G,H分别为边AB,BC,CD,AD的中点，则四边形 EFGH 的面积为 . 15.(2023·十堰)如图,□ABCD的对角线AC,BD 相交于点 O,分别以点 B,C 为圆心, AC, BD的长为半径画弧，两弧交于点P,连接BP,CP. (1)试判断四边形 BPCO 的形状，并说明理由. (2)请说明当□ABCD的对角线满足什么条件时，四边形 BPCO是正方形. C综合题 16.如图,四边形 ABCD 是正方形,点 P 在线段AC 上,点 E 在射线BC 上,且 PB=PE,连接 PD,O为线段AC的中点. 【感知】(1)如图1,当点 P 在线段AO 上时. ①易证△ABP 与△ADP 全等(不需要证明)，进而得到 PE 与 PD 的数量关系是 ②过点 P 作 PM⊥CD 于点 M,PN⊥BC于点N,易证 Rt△PNE≌Rt△PMD(不需要证明)，进而得到 PE与PD 的位置关系是 . 【探究】(2)如图2,当点 P 在线段OC 上(点P不与点O,C重合)时,试写出 PE 与 PD的数量关系和位置关系，并说明理由. 18.2.3 正方形 1. B 2. C 3.2(答案不唯一) 4.3 5.45° 6.2 7.2 8.证明:∵四边形 ABCD 是正方形,∴BC=DC,∠BCE=90°.∴∠DCF=180°-∠BCE=90°.∴∠BCE=∠DCF.在△BCE 和△DCF中,∠BCEC∠DCF,∴∠BCE△DCFF,ACEEFAS,∠EFENS,∠EFNG=∠FDC. 9. D 10. AC=BD(答案不唯一) 11.证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形.∵正方形ABCD的对角线AC,BD相交于点O,∴OD=OC,∠DOC=90°.∴平行四边形 OCED 是菱形.∵∠DOC=90°,∴菱形OCED是正方形. 12. C 13. 14.2 15.解:(1)四边形 BPCO为平行四边形.理由:∵四边形 ABCD为平行四边形， 由作图得，OB=CP,BP=OC,∴四边形BPCO为平行四边形.(2)当AC⊥BD,AC=BD时,四边形 BPCO是正方形.理由如下:∵AC⊥BD,∴∠BOC=90°.∴□BPCO 是矩形. AC,∴OB=OC.∴矩形 BPCO是正方形. 16.解:(1)①PE=PD ②PE⊥PD (2)PE=PD, ... ...