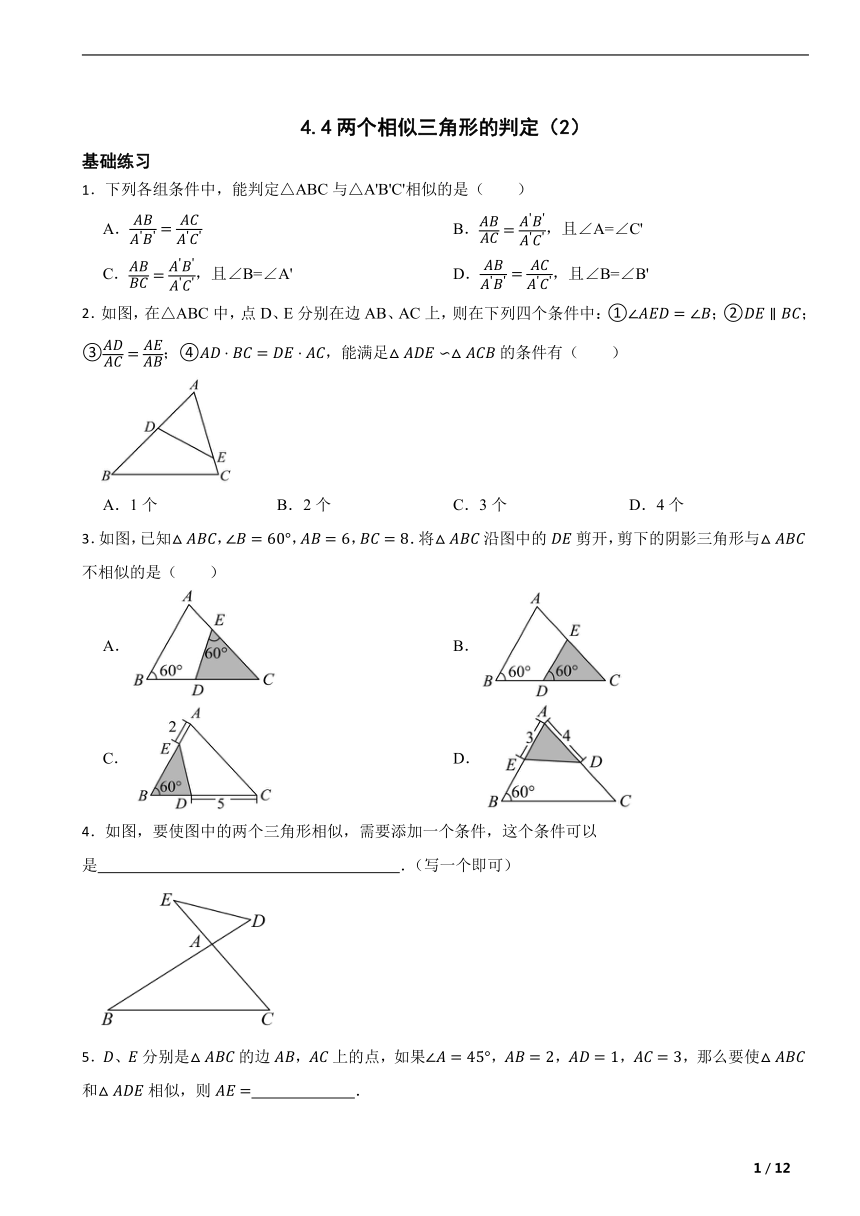
4.4两个相似三角形的判定(2) 基础练习 1.下列各组条件中,能判定△ABC与△A'B'C'相似的是( ) A. B.,且∠A=∠C' C.,且∠B=∠A' D.,且∠B=∠B' 2.如图,在△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①;②;③;④,能满足的条件有( ) A.1个 B.2个 C.3个 D.4个 3.如图,已知,,,.将沿图中的剪开,剪下的阴影三角形与不相似的是( ) A. B. C. D. 4.如图,要使图中的两个三角形相似,需要添加一个条件,这个条件可以是 .(写一个即可) 5.、分别是的边,上的点,如果,,,,那么要使和相似,则 . 6.已知:如图,△ABC中,AB=2,BC=4,D为BC边上一点,BD=1. (1)求证:△ABD∽△CBA. (2)若△ABC的周长为11,请求出AD的长. 7.如图,四边形ABCD中,AC平分∠DAB,AC2=AB AD,∠ADC=90°,E为AB的中点. (1)求证:△ADC∽△ACB; (2)若AD=4,AB=6,求的值. 提高练习 8.如图,在Rt△ABC中,∠B=90°,AD为∠BAC的角平分线,交BC于点D.过点D作交AC于点E,点P在EC上,且∠EDP=∠EDA,若EP=1,PC=4,则BD的长为( ) A. B. C. D. 9.在正方形 ABCD中,AB=4,点 E是边 AD的中点,连接 BE,将△ABE 沿 BE翻折,点 A落在点 F处,BF 与 AC交于点 H,点 O 是 AC 的中点,则 OH的长度是( ) A. B. C. D. 二、填空题 10.如图,的顶点B在反比例函数的图象上,顶点C在x轴负半轴上,轴,AB,BC分别交y轴于点D,E.若,,则 . 11.如图,在中,,,点从点出发沿方向向终点以的速度移动;同时,点从出发沿方向向终点以的速度移动.设运动时间为,当 时,与相似. 12.如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA= ,则BD的长为 . 13.如图,双曲线经过斜边的中点,交直角边于点,连接,点A的坐标为. (1)求双曲线的解析式; (2)求直线的解析式; (3)求证:. 14.如图,在正方形ABCD中,E是AD的中点,点F在CD上,且CF=3FD. (1)求证:△ABE∽△DEF. (2)△ABE与△BEF相似吗 为什么 15. 综合与实践 主题:X型晒衣架稳固性检测 步骤:如图甲是晒衣架的实物图,图乙是晒衣架侧面示意图,经测量得到立杆,,现将晒衣架完全稳固张开,横扣链成一条线段,测得. 证明与计算: (1)连接,证明:; (2)利用夹子垂挂在晒衣架上的连衣裙(夹子高度忽略不计)总长度小于多少时,连衣裙才不会拖在地面上? 16.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE CA. (1)求证:BC=CD; (2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=,求DF的长. 参考答案 1.C 2.B 3.D 4.或(答案不唯一) 5.或 6.(1)证明:∵, ∴, 且, ∴. (2)解:∵△ABC的周长为11,,,∴AC=5, ∵, ∴ ∴AD=2.5 7.(1)证明:平分, , ∵ ∴ ; (2)解:由(1)可得 点为边的中点,, , ∴ 平分, , ∴ , , , , , . 8.A 9.A 10.18 11.或 12 13.(1)解:的中点是,点的坐标为, . 双曲线经过点; , . (2)解:为直角三角形, ∴轴, ,两点的纵坐标相等,均为4,代入反比例函数解析式得:, . 设直线的解析式为, , 解得:. 直线的解析式为; (3)证明:,点的坐标为, ,,, ,, , 又, . 14.(1)证明:∵四边形ABCD为正方形, ∴∠A=∠D=90°,AB=AD=CD, 设AB=AD=CD=4a, ∵E为边AD的中点,CF=3FD, ∴AE=DE=2a,DF=a, ∴=2,=2, ∴ 又∵∠A=∠D=90°, ∴△ABE∽△DEF. (2)证明:∵△ABE∽△DEF, ∴, ∴∠AEB=∠DFE,∠ABE=∠DEF, ∵∠AEB+∠ABE=90°, ∴∠BEF=90°, ∵,∠A=90°. ∴,∠A=∠BEF=90°, ∴△ABE∽ ... ...
~~ 您好,已阅读到文档的结尾了 ~~

