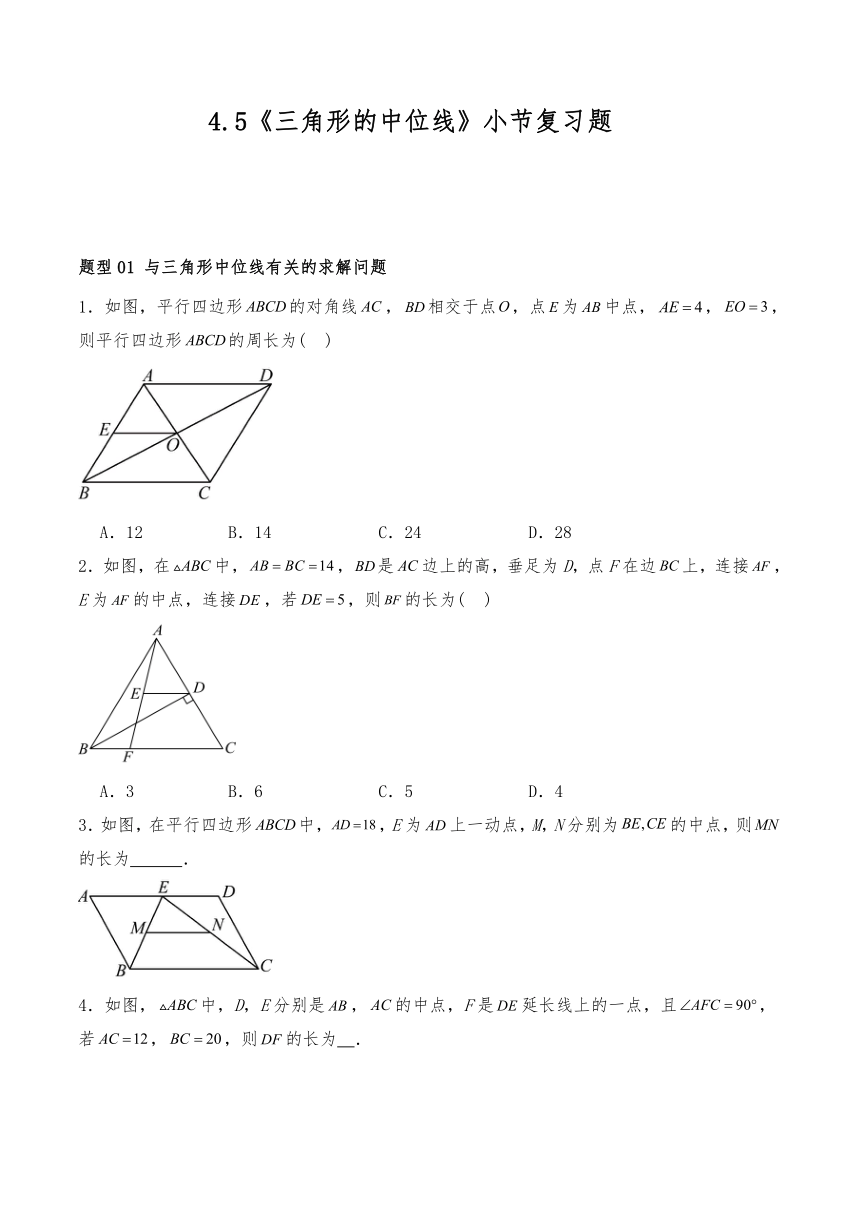
4.5《三角形的中位线》小节复习题 题型01 与三角形中位线有关的求解问题 1.如图,平行四边形的对角线,相交于点,点为中点,,,则平行四边形的周长为( ) A.12 B.14 C.24 D.28 2.如图,在中,,是边上的高,垂足为D,点F在边上,连接,E为的中点,连接,若,则的长为( ) A.3 B.6 C.5 D.4 3.如图,在平行四边形中,,E为上一动点,M,N分别为的中点,则的长为 . 4.如图,中,D,E分别是,的中点,F是延长线上的一点,且,若,,则的长为 . 5.如图,在中,D为斜边的中点,E为上一点,F为中点,若,. (1)求证:为的角平分线; (2)求的长. 题型02 三角形中位线与三角形面积问题 1.如图,是的中位线,是的中点,的延长线交于点,若的面积为2,则的面积为( ) A.4 B.6 C.8 D.9 2.如图,在中,平分,于点D,且,则的面积为( ) A.4 B.5 C.6 D.8 3.如图,在与中,点,,分别是,,的中点,若的面积等于,则的面积为 4.如图,是的中位线,M是的中点,的延长线交于N,那么 ,S DMN:S四边形ANME = . 5.公股定理神奇而美丽,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:两个全等的直角三角板 和直角三角板 ,顶点F在边止,顶点C、D重合,连接 、.设、交于点G., , ( ),. 请你回答以下问题: (1)请猜想与的位置关系,并加以证明. (2)填空: =_____(用含有c的代数式表示) (3)请尝试利用此图形证明勾股定理. 题型03 与三角形中位线有关的证明 1.如图,四边形中,点、、、分别是线段、、、的中点,则四边形的周长( ) A.只与、的长有关 B.只与、的长有关 C.只与、的长有关 D.与四边形各边的长都有关 2.如图,在中,,,,点D,E,F分别是,,的中点,连接,,则四边形的周长为( ) A.6 B.9 C.11 D.13 3.如图,在ABC中,点D,E,F分别是边,,上的中点,且,,则四边形的周长等于 . 4.如图,在中,,,分别为,的中点,平分,交于点,若,,则的长为 . 5.如图,已知平行四边形ABCD,、相交于点O,延长到点E,使,连接. (1)求证:四边形是平行四边形: (2)连接,交于点F,连接,判断与的数量关系,并说明理由. 题型04 三角形中位线的实际应用 1.如图,施工队打算测量,两地之间的距离,但,两地之间有一个池塘,于是施工队在处取点,连接,,测量,的中点之间的距离是,则两地之间距离为( ) A. B. C. D. 2.如图,为测量池塘两端的距离,可先在平地上取一个点,从点不经过池塘可以直接到达点和,连接,,分别取、的中点,,连接后,量出的长为12米,那么就可以算出,的距离是( ) A.36米 B.24米 C.12米 D.6米 3.如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到,的中点D,E,并且测出的长为,则A,B间的距离为 . 4.某地需要开辟一条隧道,隧道的长度无法直接测量,如图所示,在地面上取一点,使到、两点均可直接到达,测量找到和的中点、,测得的长为1800米,则隧道的长度为 米. 5.如图1,在平行四边形中,点E、F分别为,的中点,点G,H在对角线上,且. (1)求证:四边形是平行四边形. (2)如图2,连接交于点O,若,,,求的长. 题型05 三角形中位线的综合问题 1.如图1,中,,是的中位线,动点从点出发,以每秒的速度沿的方向运动,到达点时停止.设点运动(秒)时,的面积为,如图2是关于的函数图象,则图2中,的值分别是( ) A., B., C., D., 2.如图,在中,,点在上,为的中点,连结,,,,则的长为( ) A. B.3 C. D.4 3.如图.点A、B的坐标分别为 ,C为坐标平面内一点,,点为线段的中点,连接 ... ...
~~ 您好,已阅读到文档的结尾了 ~~