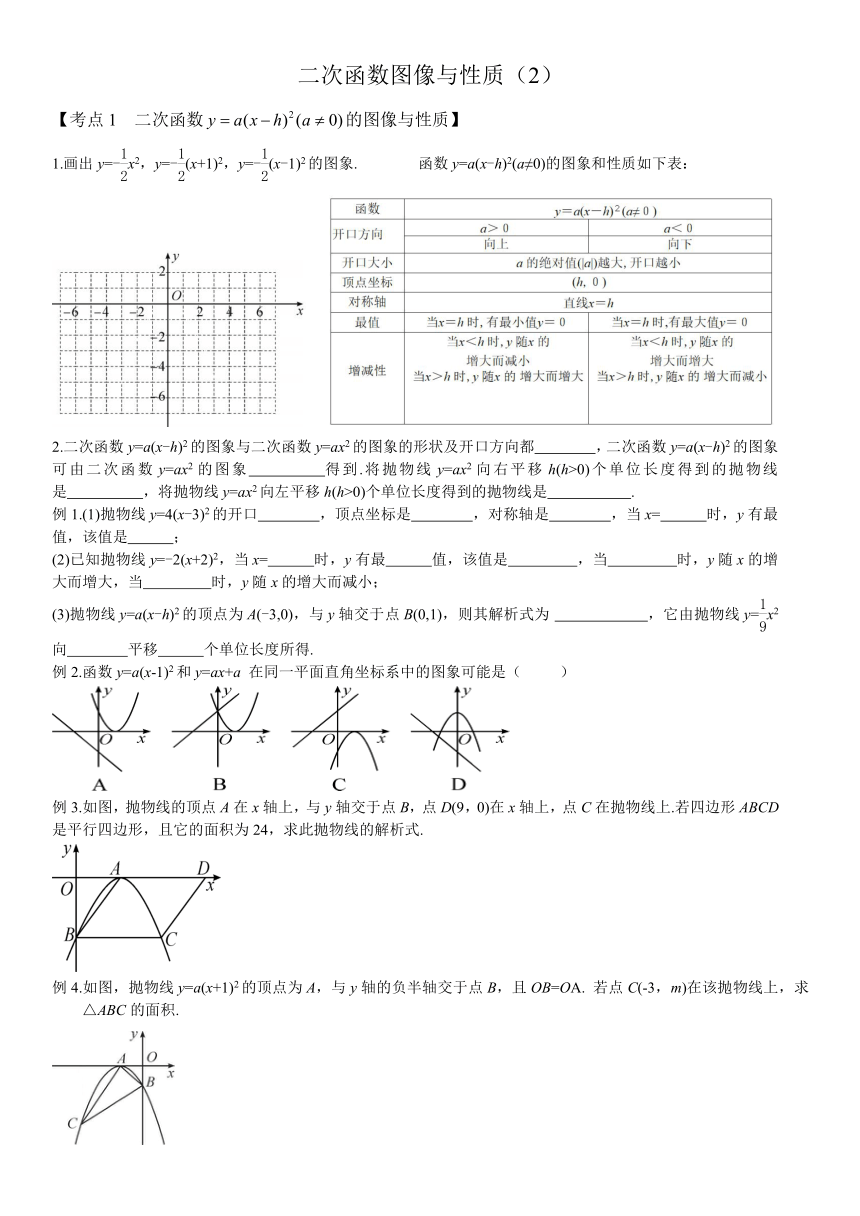
二次函数图像与性质(2) 【考点1 二次函数的图像与性质】 1.画出y=-x2,y=-(x+1)2,y=-(x-1)2的图象. 函数y=a(x-h)2(a≠0)的图象和性质如下表: 2.二次函数y=a(x-h)2的图象与二次函数y=ax2的图象的形状及开口方向都 ,二次函数y=a(x-h)2的图象可由二次函数y=ax2的图象 得到.将抛物线y=ax2向右平移h(h>0)个单位长度得到的抛物线是 ,将抛物线y=ax2向左平移h(h>0)个单位长度得到的抛物线是 . 例1.(1)抛物线y=4(x-3)2的开口 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值,该值是 ; (2)已知抛物线y=-2(x+2)2,当x= 时,y有最 值,该值是 ,当 时,y随x的增大而增大,当 时,y随x的增大而减小; (3)抛物线y=a(x-h)2的顶点为A(-3,0),与y轴交于点B(0,1),则其解析式为 ,它由抛物线y=x2向 平移 个单位长度所得. 例2.函数y=a(x-1)2和y=ax+a 在同一平面直角坐标系中的图象可能是( ) 例3.如图,抛物线的顶点A在x轴上,与y轴交于点B,点D(9,0)在x轴上,点C在抛物线上.若四边形ABCD是平行四边形,且它的面积为24,求此抛物线的解析式. 例4.如图,抛物线y=a(x+1)2的顶点为A,与y轴的负半轴交于点B,且OB=OA. 若点C(-3,m)在该抛物线上,求△ABC的面积. 练习1.(1)抛物线y=-3(x+2)2向左平移1个单位长度后,所得抛物线的解析式为 ;向右平移2个单位长度后,所得抛物线的解析式为 . (2)平行于x轴的直线与抛物线y=a(x-2)2的一个交点坐标为(-1,2),则另一个交点坐标为 . (3)已知抛物线y=a(x-h)2的对称轴为直线x=-2,且经过点 (1,-3),则此抛物线的解析式是 . 练习2.如图是一副眼镜镜片下半部轮廓对应的两条抛物线,它们关于y轴对称,AB∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm.求右轮廓线DFE的函数解析式. 【考点2 二次函数的图像与性质】 1.画出函数y= - (x+2)2-1和y= - (x-4)2+2的图象, 函数y=a(x-h)2+k(a≠0)的图象和性质如下表: 思考其图象可由y=-x2的图象怎样平移得到? 例1.(1)对于二次函数y=(x-2)2+1,下列说法错误的是( ) A. y的最小值为1 B. 图象的顶点坐标为(2,1),对称轴为直线x=2 C. 当x<2时,y的值随x的增大而增大,当x≥2时,y的值随x的增大而减小 D. 它的图象可以由y=x2的图象向右平移2个单位长度,再向上平移1个单位长度得到 (2)将抛物线y=-2x2+1向右平移1个单位长度,再向上平移1个单位长度所得抛物线的解析式为 . (3)已知A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+k上的三点,则y1,y2,y3的大小关系是 . 例2.如图,有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立平面直角坐标系.(1)请直接写出O,A,M三点的坐标;(2)求此抛物线形桥洞的解析式. 例3.要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1 m处达到最高,高度为3 m,水柱落地处离池中心3 m,水管应安装多长? 练习1.(1)已知点A(1,y1),B(2,y2)在抛物线y=-(x+1)2+2上,则下列结论正确的是( ) A. 2>y1>y2 B. 2>y2>y1 C. y1>y2>2 D. y2>y1>2 (2)已知二次函数y=a(x-2)2+k 的图象与x轴交于A(-1,0),B两点,则线段AB的长为 . (3)将抛物线y=3(x+2)2-4向右平移3个单位长度,再向上平移2个单位长度,得到抛物线的解析式是 . (4)抛物线y=2(x+9)2-3的顶点坐标是 . (5)如图是二次函数y=(x+m)2+n的图象,则一次函数y=mx+n的图象不经过第 象限. (5)题图 (6)题图 (6)如图是抛物线y=a(x+1)2+2的一部分,则该抛物线在y轴右侧部分与x轴的交点的坐标是 . 练习2.如图,排球运动员站在点O处练习发球,将球从点O正上方2 m处的点A发出,把球看成点,其运行的高度y(单位:m)与运行的水平距离x( ... ...
~~ 您好,已阅读到文档的结尾了 ~~