2.4线段的和与差 同步训练（含答案）2025-2026学年数学冀教版（2024）七年级上册

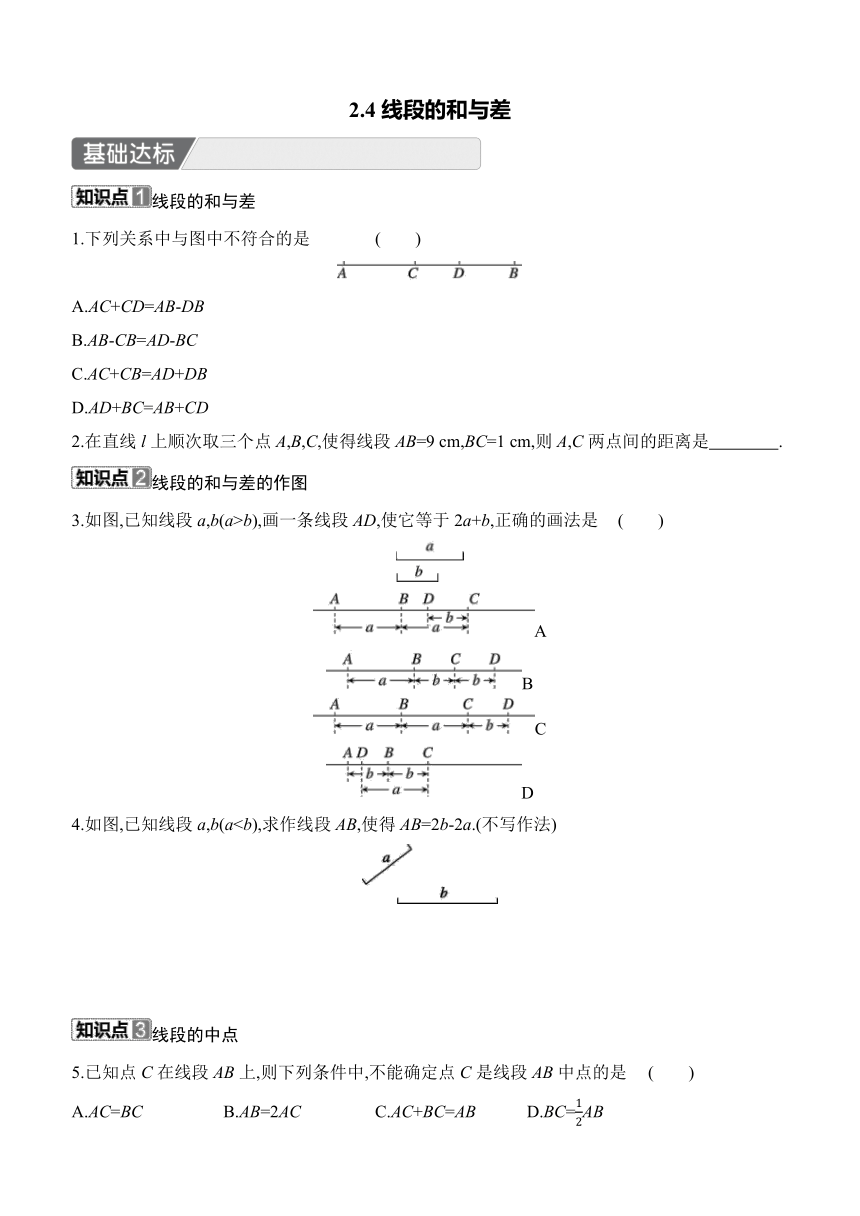
2.4线段的和与差 线段的和与差 1.下列关系中与图中不符合的是 (　　) A.AC+CD=AB-DB B.AB-CB=AD-BC C.AC+CB=AD+DB D.AD+BC=AB+CD 2.在直线l上顺次取三个点A,B,C,使得线段AB=9 cm,BC=1 cm,则A,C两点间的距离是　　　　. 线段的和与差的作图 3.如图,已知线段a,b(a>b),画一条线段AD,使它等于2a+b,正确的画法是 (　　) A B C D 4.如图,已知线段a,b(ac),则ND的长度为 (　　) A.a+2b-2c B.a+2b+2c C.a+b-c D.a+2b-c 6.如图,已知线段AB=16 cm,点M在线段AB上,AM∶BM=1∶3,P,Q分别为AM,AB的中点,则PQ的长为　　　　. 7.(新考法)如图,线段AB表示一条对折以后的绳子,现从P处把绳子剪断,剪断后的各段绳子中最长的一段为32 cm;若AP=PB,则这条绳子的原长为　　　　 cm. 8.(教材P77习题A组T3变式)已知线段a,b,c(a>c),如图所示,作线段AB,使AB=a+b-c.(不写作法) 9.如图,已知点 A,B,C,D,E在同一条直线上,且AC=BD,E是线段BC的中点. (1)判断点E是不是线段AD的中点,并说明理由. (2)当AD=10,AB=3时,求线段BE的长度. 10.(抽象能力)已知平面上有一条线段AB=10 cm,探讨下列问题: (1)平面上是否存在一点C,使它到A,B两点的距离之和等于8 cm 说明理由. (2)平面上是否存在一点D,使它到A,B两点的距离之和等于10 cm 若存在,它的位置唯一吗 (3)当点E到A,B两点的距离之和等于20 cm时,点E一定在直线AB外吗 请举例说明. 【详解答案】 基础达标 1.B　2.10 cm　3.C 4.解:如图,线段AB即为所作. 5.C　6.A 7.解:因为M是AC的中点,AM=2 cm, 所以AM=CM=2 cm. 所以AC=AM+CM=2+2=4(cm). 又因为AB=10 cm, 所以BC=AB-AC=10-4=6(cm). 能力提升 1.D　解析:由题图可知,AC=AD-CD,所以△表示CD.故A选项不符合题意.AC=AB+BC,所以表示AB.故B选项不符合题意.AD-AB=BD,BC+CD=BD,所以□表示CD.故C选项不符合题意.AC-AB=BC,BD-CD=BC,所以○表示CD.故D选项符合题意.故选D. 2.C　解析:若点C在点B的右侧,则AC=AB+BC=8,若点C在点B的左侧,则AC=AB-BC=4,综上所述AC=4或AC=8.故选C. 3.C　解析:设BC=x,则AC=2BC=2x.所以AB=AC+BC=2x+x=3x.因为AB=12,所以3x=12,所以BC=x=4.因为M为AB的中点,所以AM=MB=AB=6.所以MC=MB-BC=6-4=2.故选C. 4.B　解析:当点C是线段AB的“巧点”时,可能有BC=2AC,AC=2BC,AB=2AC=2BC三种情况:①BC=2AC时,AC=AB=×12=4;②AC=2BC时,AC=AB=×12=8;③AB=2AC=2BC时,AC=AB=×12=6.故选B. 5.A　解析:如图: 因为AB=a,BC=CD=b,所以 AD=AB+BC+CD=a+b+b=a+2b.因为AE=EN=c,所以ND=AD-AE-EN=a+2b-c-c=a+2b-2c.故选A. 6.6 cm ... ...