第11讲选修4-1《几何证明选讲》模块综合检测题Word版含解析

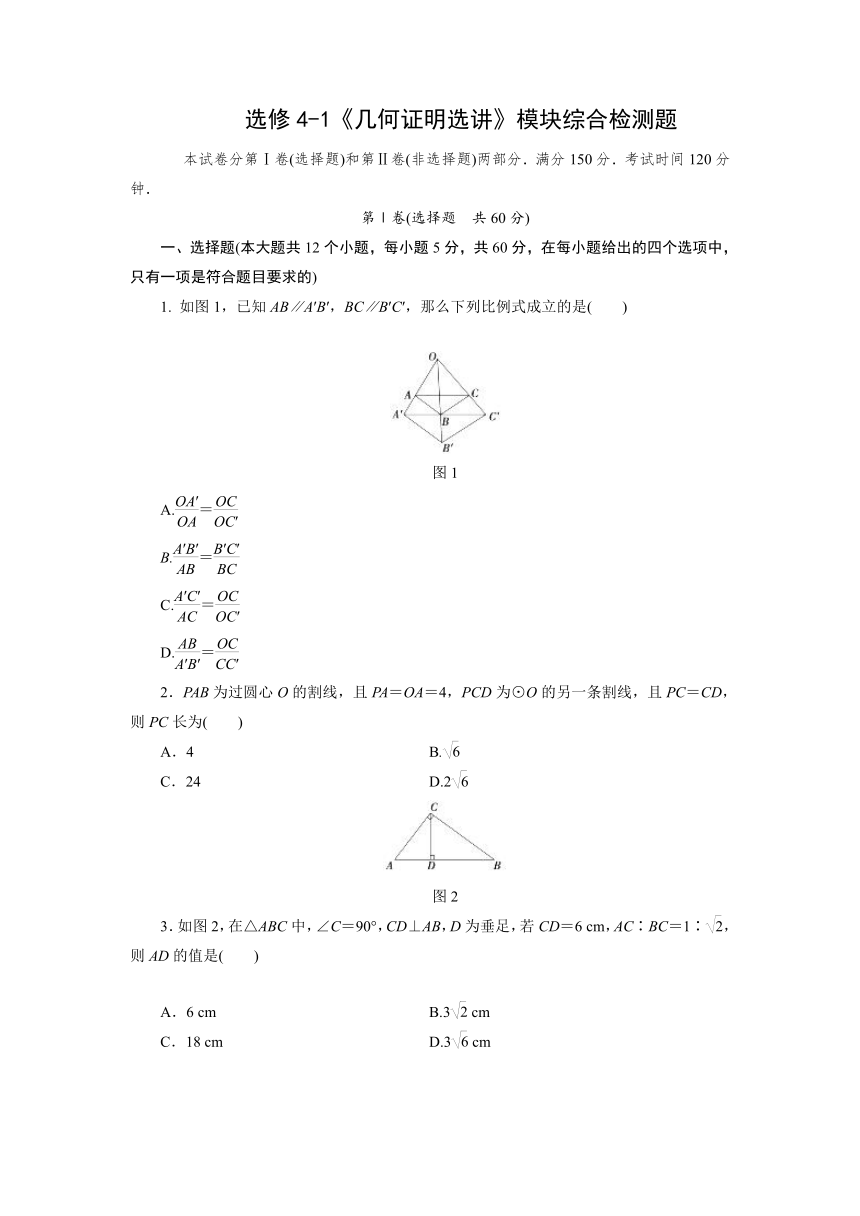
选修4-1《几何证明选讲》模块综合检测题 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟． 第Ⅰ卷(选择题　共60分) 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1. 如图1，已知AB∥A′B′，BC∥B′C′，那么下列比例式成立的是(　　) 图1 A.＝ B.＝ C.＝ D.＝ 2．PAB为过圆心O的割线，且PA＝OA＝4，PCD为⊙O的另一条割线，且PC＝CD，则PC长为(　　) A．4　　　　　　　 B. C．24 D.2 图2 3．如图2，在△ABC中，∠C＝90°，CD⊥AB，D为垂足，若CD＝6 cm，AC∶BC＝1∶，则AD的值是(　　) A．6 cm B.3 cm C．18 cm D.3 cm 图3 4．如图3，⊙O内切于△ABC，切点分别为D、E、F.已知∠B＝50°，∠C＝60°，连接OE、OF、DE、DF，那么∠EDF等于(　　) A．40° B.55° C．65° D.70° 图4 5．如图4，平行四边形ABCD中，AE∶EB＝1∶2，若△AEF的面积等于2 cm2，则△CDF的面积等于(　　) A．16 cm2 B.18 cm2 C．20 cm2 D.22 cm2 图5 6．如图7，点C在以AB为直径的半圆上，连接AC、BC，AB＝10，tan∠BAC＝，则阴影部分的面积为(　　) A.π B.π－24 C．24 D.＋24 图6 7．如图6，用与底面成30°角的平面截圆柱得一椭圆截线，则该椭圆的离心率为(　　) A. B. C. D.非上述结论 8．如图7所示，∠ACB＝90°，CD⊥AB于点D，以BD为直径的圆与BC交于点E，则(　　) 图7 A．CE·CB＝AD·DB B.CE·CB＝AD·AB C．AD·AB＝CD2 D.CE·EB＝CD2 图8 9．如图8，AB、CD是圆O的两条弦，且AB是线段CD的中垂线，已知AB＝6，CD＝2，则线段AC的长度为(　　) A．5　　　　　　　 B. C. D.3 图9 10．如图9，E，C分别是∠A两边上的点，以CE为直径的⊙O交∠A的两边于点D，点B，若∠A＝45°，则△AEC与△ADB的面积比为(　　) A．2∶1 B.1∶2 C.∶1 D.∶1 11. 图10 如图10所示，球O与圆柱的上、下底面以及侧面均相切，用一平面去截圆柱和球，得到的截面图有可能是(　　) A．①②④ B.①②③ C．②③④ D.①②③④ 12．如图11，已知△ABC中，＝，＝，AD、BE交于F，则·的值为 (　　) 图11 A. B. C. D. 第Ⅱ卷(非选择题　共90分) 二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 图12 13．如图12，点E、F分别在AD、BC上，已知CD＝2，EF＝3，AB＝5，若EF∥CD∥AB, 则等于_____． 图13 14．如图13，PT切⊙O于点T，PA交⊙O于A、B两点，且与直径CT交于点D.CD＝2，AD＝3，BD＝6，则PB＝_____. 15．一平面与半径为4的圆柱面相截，截面的Dandelin双球的球心距离为12，则截线椭圆的离心率e＝_____. 图14 16．已知如图14，△ABC中，边AC上一点F分AC为＝，BF上一点G分BF为＝，AG的延长线与BC交于点E，则BE∶EC＝_____. 三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤) 17．(本小题满分10分)已知如图15，DE∥BC，四边形DEFG是平行四边形．求证：AH∥DG. 图15 18．(本小题满分12分)如图16，AB为⊙O的直径，AD、BC是⊙O的切线，DC切⊙O于E，并与AD、BC分别交于D、C两点，BD与AC交于点F，求证：FE∥A D. 图16 19．(本小题满分12分)如图17，圆O1与圆O2内切于点A，其半径分别为r1与r2(r1＞r2)．圆O1的弦AB交圆O2于点C(O1不在AB上)．求证：AB∶AC为定值． 图17 20．(本小题满分12分)如图18所示，已知⊙O1与⊙O2相交于A，B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1，⊙O2于点D，E，DE与AC相交于点P. (1)求证：AD∥EC； (2)若AD是⊙O2的切线，且PA＝6，PC＝2，BD＝9，求AD的长． 图18 21．(本小题满分12分)如图19，已知⊙O和⊙M相交于A、B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为弧BC中点，连接AG分别交 ... ...