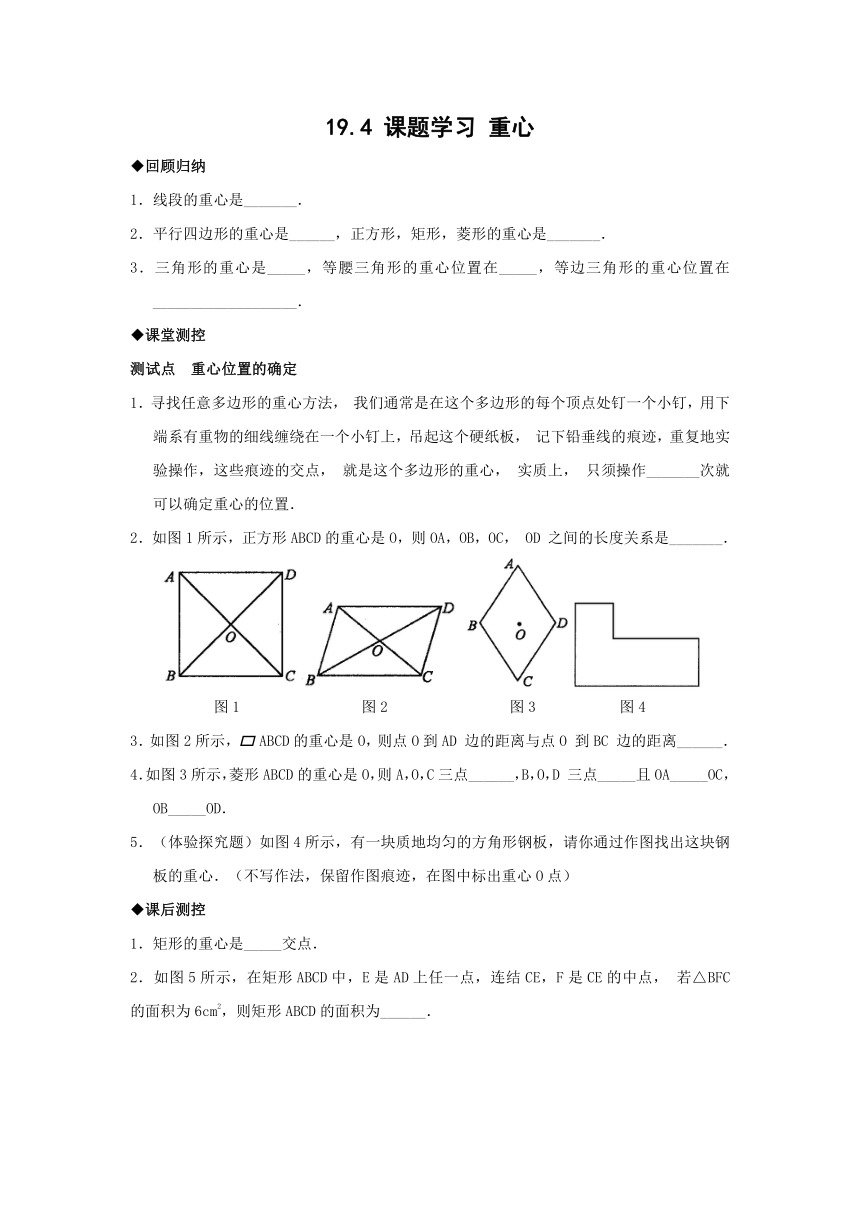
19.4 课题学习 重心(含答案)

19.4 课题学习 重心 ◆回顾归纳 1．线段的重心是_____． 2．平行四边形的重心是_____，正方形，矩形，菱形的重心是_____． 3．三角形的重心是_____，等腰三角形的重心位置在_____，等边三角形的重心位置在_____． ◆课堂测控 测试点 重心位置的确定 1．寻找任意多边形的重心方法，我们通常是在这个多边形的每个顶点处钉一个小钉，用下端系有重物的细线缠绕在一个小钉上，吊起这个硬纸板，记下铅垂线的痕迹，重复地实验操作，这些痕迹的交点，就是这个多边形的重心，实质上，只须操作_____次就可以确定重心的位置． 2．如图1所示，正方形ABCD的重心是O，则OA，OB，OC，OD之间的长度关系是_____． 图1 图2 图3 图4 3．如图2所示，ABCD的重心是O，则点O到AD边的距离与点O到BC边的距离_____． 4．如图3所示，菱形ABCD的重心是O，则A，O，C三点_____，B，O，D三点_____且OA_____OC，OB_____OD． 5．（体验探究题）如图4所示，有一块质地均匀的方角形钢板，请你通过作图找出这块钢板的重心．（不写作法，保留作图痕迹，在图中标出重心O点） ◆课后测控 1．矩形的重心是_____交点． 2．如图5所示，在矩形ABCD中，E是AD上任一点，连结CE，F是CE的中点，若△BFC的面积为6cm2，则矩形ABCD的面积为_____． 图5 图6 图7 图8 3．如图6所示，已知任意直线L把ABCD分成两部分，要使这两部分的面积相等，直线L所在位置需满足的条件是_____．（只需填上一个你认为合适的条件） 4．如图7所示，在五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将五边形ABCDE分成面积相等的两部分的直线有_____条，满足条件的直线可以这样确定：_____． 5．如图8所示，矩形ABCD的重心是O，则图中共有_____对全等三角形． 6．下列说法错误的是（ ） A．线段的重心在线段的中垂线上 B．菱形的重心是菱形一条对角线的交点 C．矩形的重心是矩形两条对称轴的交点 D．正方形的重心是正方形内任一点 7．如图所示，在△ABC中，AB=AC，G是△ABC的重心，过G点作GD⊥AB，GE⊥AC，垂足为D，E． （1）猜想：GD_____GE； （2）试对上面的猜想加以证明． 8．在一次数学探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等． （1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有_____组； （2）请在下图的三个平行四边形中画出满足小强分割方法的直线； （3）由上述实验操作过程，你发现所画的两条直线有什么规律？ ( http: / / ) ◆拓展创新 9．探究下列问题： （1）在图（1）给出的四个正方形中，各画出一条直线（依次是：水平方向的直线，竖直方向的直线，与水平方向成45°角的直线和任意的直线），将每个正方形都分割成面积相等的两部分； （2）一条竖直方向的直线m以及任意的直线n，在由左向右平移的过程中，将正六边形分成左右两部分，其面积分别记为S1和S2． ①请你在图（2）中相应图形下方的横线上分别填写S1与S2的数量关系（用“<”、“＝”或“>”连接）； ②请你在图（3）中分别画出反映S1与S2三种大小关系的直线n，并在相应图形下方的横线上分别填写S1与S2的数量关系式（用“<”、“＝”或“>”连接）． （3）是否存在一条直线，将一个任意的平面图形（如图（4）分割成面积相等的两部分，请简略说出理由． 答案: 回顾归纳 1．线段的中点 2．对角线的交点，对角线的交点 3．三条中线的交点，底边的高线上，每条边的高的交点 课堂测控 1．两 2．OA=OB=OC=OD 3．相等 4．在一条直线上，在一条直线上，=，= 5．如图． 课后测控 1．对角线 2．24cm2 3．过AC与BD的交点 4．无数，设该直线与边DE，AB的交点分别为P，Q，线段PQ的中点为O，则经过点O与边DE，AB相交的任意一条直线均可将该五边形的面积均分 5．4 6 ... ...