高中数学思维导图PDF版

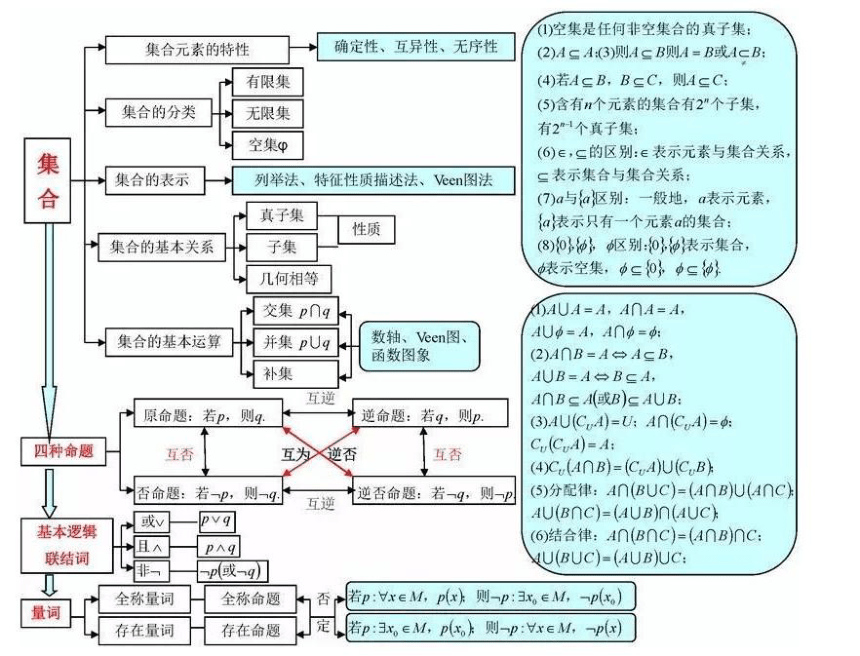
空集是任何非空集合的真子集 集合元素的特性 确定性、互异性、无序性((2)44(3则AB则A=B或cB 有限集 (4)若A∈B,B∈C,则 集合的分类 无限集 (5)含有n个元素的集合有2”个子集, 有2”1个真子集 空集φ 集 (6)∈,g的区别:∈表示元素与集合关系, 集合的表示 列举法、特征性质描述法、n图法]s表示集合与集合关系 合 (7)a与{a区别:一般地,a表示元素 真子集 性质 a法表示只有一个元素a的集合 集合的基本关系子集 (8)@},区别:和师法表示集合, 几何相等 ￠示空集,归φ 交集p∩q )4UA=A,A∩A=A 集合的基本运算十并集pUqH数轴、ecn图、 A∪φ=A,4∩中= ∏函数图象 (2)A∩B=AA∈B, 补集 AUB=A台BgA, 互逆 原命题:着,则小 ∩BcA或B)cAUB: 逆命题:若则64U(A=4An(C,A)= 四种命题 互否 互为逆否 互否 Cu(cua)=A (4)C(4nB)=(CA儿J(CB) 命题:若→,则少互趣十逆否命题:若=9,则(5)分配律:4∩(BU)=(nBu(nc AU(B∩C)=(AUBn(UC 基本逻辑 或 (6)结合律:A∩(B∩C)=(∩B∩C 联结词 U(BUC)=(UB儿C 全称量词全称命题否产若p:x∈M,p)则-P:3x∈M,-px) 量词 存在量词H存在命题定以若p:3∈M,px)则-p:vr∈M,x) 基本性质 不等关系与不等式比较大小问题作差或作商 求解范围问题 元二次不等式及其解法借助二次函数图象 、利用三个“二次”间的关系 二元一次不等式(组)与平面区域 几何意义:z是直线 可行域 +by-z=0在x轴截距 的a倍,y轴上截距的 简单的线性规划问题 目标函数 构造斜率:z= b倍 不 应用题 构造距离:=√x-a)+(-b 式 基不每式最值]气和为定值,积有最大值:积为定值,和有最小值“一正三定三相等 √ab≤ a+b 变形 2s、aba+bs,a2+b2 +b 2 2 元一次a>b 分谷>0.a<0.a=0(b≥0.b<0)讨论 一元二次不等式 分a0a0.A0△=0△-0讨论 ax2+bx+c>0(a≠0) x系数化为正,“穿根法”,奇穿偶不字 元高次不等式 解不等式 (.sXr-x,)(x-x,)>0(o) g() 8)20分f(x)(x)>0(x) ≥0f(x)g(x)20且g(x)≠0 分式不等式 (xg(x)=-8(x)g(x)→f(x)>g(x减或/(x)<-g(x) 解不等式组 绝对值不等式 /(r>lg(rek(x'>g(x) 利用性转化为代数不等式,)形如-+-4<,可分段讨论或用 指数对数不等式 飞底数a的讨论 绝对值几何意义求解