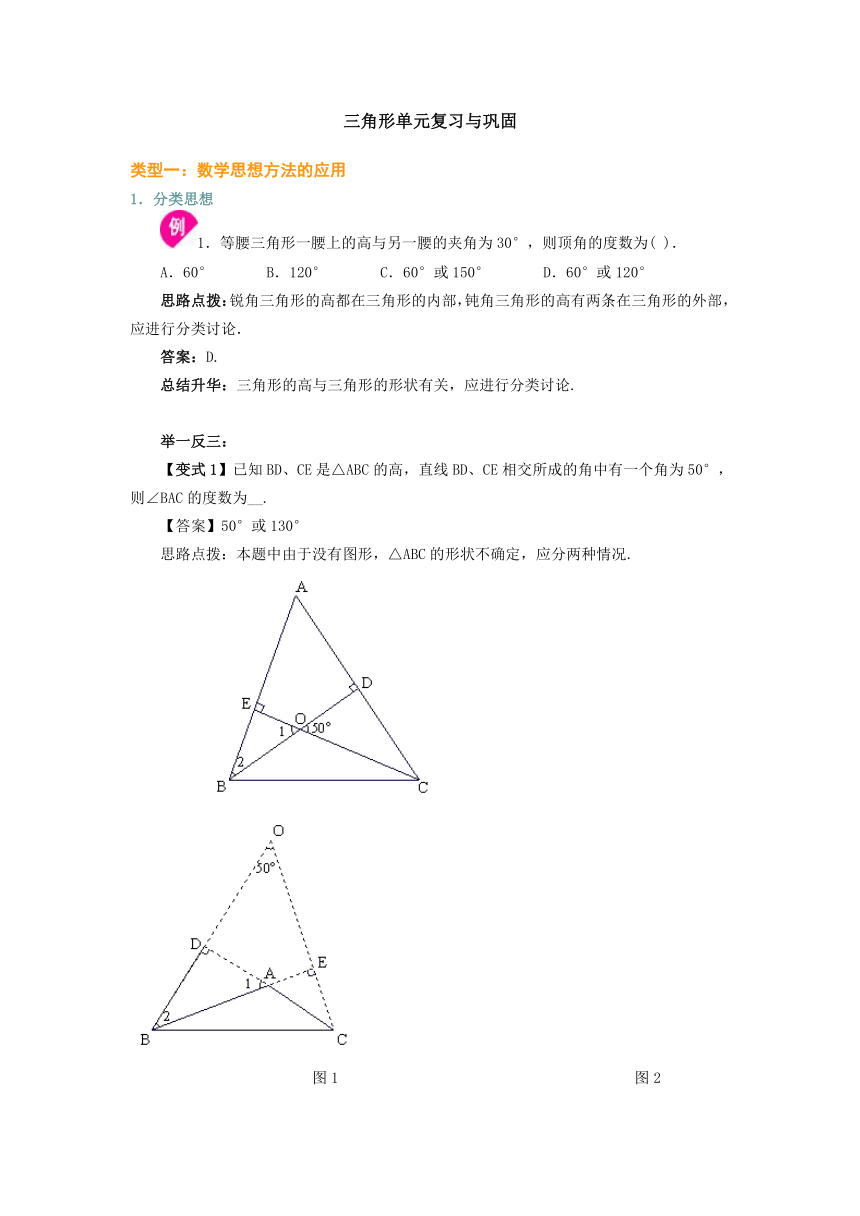
三角形单元复习与巩固

三角形单元复习与巩固 类型一：数学思想方法的应用 1．分类思想 　　1．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为( )． 　　A．60°　　　 B．120°　　　 C．60°或150°　　　 D．60°或120° 　　思路点拨：锐角三角形的高都在三角形的内部，钝角三角形的高有两条在三角形的外部，应进行分类讨论． 　　答案：D. 　　总结升华：三角形的高与三角形的形状有关，应进行分类讨论. 　　举一反三： 　　【变式1】已知BD、CE是△ABC的高，直线BD、CE相交所成的角中有一个角为50°，则∠BAC的度数为__. 　　【答案】50°或130° 　　思路点拨：本题中由于没有图形，△ABC的形状不确定，应分两种情况. 　　　　　　　　　 　　　　　　　　　　　　图1　　　　　　　　　　　　　　　　　　　 图2 　　如图1所示，△ABC是锐角三角形，因为BD、CE是△ABC的高，所以△BOE、△BAD都是直角三角形，则　　∠A+∠2＝90°，∠1+∠2＝90°，所以∠A＝∠1＝50°，即∠BAC＝50°. 　　如图2所示，△ABC是钝角三角形，因为BD、CE是△ABC的高，所以△ABD、△OBE都是直角三角形，则　　∠1+∠2＝90°，∠O+∠2＝90°，所以∠1＝∠O＝50°，所以∠BAC＝180°－∠1＝180°－50°＝130°. 　　【变式2】有四条线段，它们的长分别为1cm，2cm，3cm，4cm，从中选出三条组成三角形，正确的选法有(　　) 　　A、1种　　　　B、2种　　　C、3种　　　　D、4种 　　解析：从四条线段中任选三条，共有4种选法：①1cm，2cm，3cm；②1cm，2cm，4cm；③1cm，3cm，4cm；④2cm，3cm，4cm，其中能构成三角形的选法只有④2cm，3cm，4cm，故选A。 　　答案：A 　　总结升华：判断三条线段能否构成三角形，只要检验两条较短(小)线段之和能否大于第三条线段即可。若大于，则能构成三角形；否则，不能。 2．转化思想 　　2．(1)如图1是一个五角星ABCDE，请算出∠A+∠B+∠C+∠D+∠E的大小. 　　　　　　(2)如图2，3，4，5的变式图形中，上面的结论成立吗？为什么 　　思路点拨：本题是一题多变题，先求出图1中各角之和，其他图形是否有相同的结论同理可证. 　　　　　　　 　　　　　　　　　 图1 　　　　　　　　　　　　图2 　　　　　　　　　　　　图3 　　　　　　　　　　　　 　　　　　　　　　　　　 图4 　　　　　　　　　　　　　　　　　　图5 　　解析：(1)∠A+∠B+∠C+∠D+∠E＝180°. 　　　　　　 理由：∵∠C+∠E＝∠1，∠B+∠D＝∠2，∴∠A+∠B+∠C+∠D+∠E＝∠1+∠2+∠A＝180°. 　　　　　(2)在图2,3,4,5中，仍有∠A+∠B+∠C+∠D+∠E＝180°. 　　　　　　 理由同(1).在图2中，∠B为∠EBD. 　　　　　　 在图4中，延长CE与AD交于一点，则∠A+∠C＝∠1，∠B+∠E＝∠2， 　　　　　　 ∴∠A+∠B+∠C+∠D+∠E＝∠1+∠2+∠D＝180°. 　　总结升华：运动变化的问题一直是中考的热点问题，处理这类问题的关键是抓住变化中不变的量. 将所求转化到我们所熟悉的知识点上，再求解. 　　举一反三： 　　【变式1】如下图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝＿＿＿。 　　　　　　　　　　　　　　　　 　　解析：如下图，∠2＝∠1＝∠C＋∠B＋∠A，又∠2＋∠E＋∠F＋∠D＝360°， 　　　　　则∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°。 　　答案：360°。 　　　　　　　　　　　 　　【变式2】一个零件的形状如下图所示，规定∠A＝90°，∠B和∠C分别是32°和21°，检验工人量得　　∠BDC＝149°，就断定这个零件不合格，请你运用三角形的有关知识说明零件不合格的原因。 　　　　　　　　　　　　　　　　　　　　　 　　解析：连结AD，并延长至点E，如下图： 　　　　　　　　　　 　　　　　因为∠CDE＝∠CAD＋∠C，∠BDE＝∠BAD＋∠B(三角形 ... ...