暑期特训：图形变换（2）

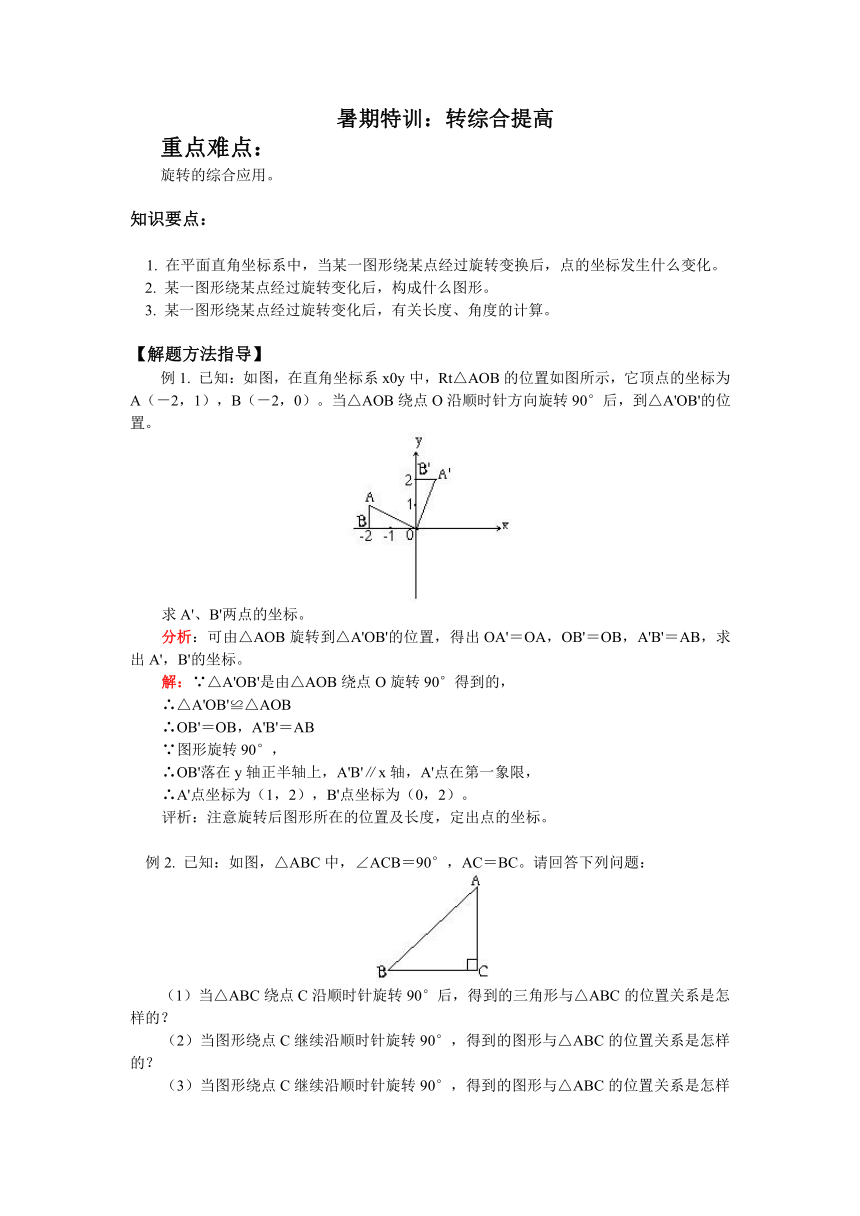
暑期特训：转综合提高 重点难点： 旋转的综合应用。 知识要点： 1. 在平面直角坐标系中，当某一图形绕某点经过旋转变换后，点的坐标发生什么变化。 2. 某一图形绕某点经过旋转变化后，构成什么图形。 3. 某一图形绕某点经过旋转变化后，有关长度、角度的计算。 【解题方法指导】 例1. 已知：如图，在直角坐标系x0y中，Rt△AOB的位置如图所示，它顶点的坐标为A（－2，1），B（－2，0）。当△AOB绕点O沿顺时针方向旋转90°后，到△A'OB'的位置。 求A'、B'两点的坐标。 分析：可由△AOB旋转到△A'OB'的位置，得出OA'＝OA，OB'＝OB，A'B'＝AB，求出A'，B'的坐标。 解：∵△A'OB'是由△AOB绕点O旋转90°得到的， ∴△A'OB'≌△AOB ∴OB'＝OB，A'B'＝AB ∵图形旋转90°， ∴OB'落在y轴正半轴上，A'B'∥x轴，A'点在第一象限， ∴A'点坐标为（1，2），B'点坐标为（0，2）。 评析：注意旋转后图形所在的位置及长度，定出点的坐标。 例2. 已知：如图，△ABC中，∠ACB＝90°，AC＝BC。请回答下列问题： （1）当△ABC绕点C沿顺时针旋转90°后，得到的三角形与△ABC的位置关系是怎样的？ （2）当图形绕点C继续沿顺时针旋转90°，得到的图形与△ABC的位置关系是怎样的？ （3）当图形绕点C继续沿顺时针旋转90°，得到的图形与△ABC的位置关系是怎样的？ 分析：由于△ABC是等腰直角三角形，当它绕点C沿顺时针方向旋转90°后，可画出图形，然后再作判断；其余两问同样处理。 解：（1）当△ABC绕点C沿顺时针旋转90°后，得到△A'B'C（如图1）， ∵△A'B'C≌△ABC，∠A'CB'＝∠BCA＝90°， ∴△A'B'C与△BAC成轴对称。 （2）当继续绕点C沿顺时针旋转90°后，得到△A'CA''。（图2） ∵△A'CA''≌△BAC 且A'、C、B三点在一条直线上，A'C＝BC， A''、C、A三点在一条直线上，A''C＝AC， ∴△A'CA''与△BCA成中心对称。 （3）当继续绕点C沿顺时针旋转90°后，得到△A''BC（图3）。 同样可知△A''BC与△ABC成轴对称。 评析：画出示意图便于观察。 例3. 已知：如下图，△ABC是等边三角形。 （1）当△ABC绕点C沿顺时针旋转60°后，图中得到一个什么图形？ （2）继续绕点C沿顺时针旋转60°，图中得到一个什么图形？ （3）当△ABC绕点C沿顺时针连续旋转五次后，得到一个什么图形？ 分析：我们仍通过画图，分析图形的特征，然后作出判断。 解：（1）当△ABC绕点C沿顺时针旋转60°后，得到△CAA'（图1）。 ∵∠BAC＝∠ACA'＝60°， ∴AB∥A'C， ∵∠ACB＝∠A'AC＝60°， ∴AA'∥BC ∴四边形ABCA'是平行四边形 又AB＝ A'A， ∴四边形ABC A'是菱形。 （2）继续绕点C沿顺时针旋转60°后，得到△A''CA'（图2）。 ∵AA'∥BA''，AB＝A'A''， ∴四边形BAA'A''是等腰梯形。 （3）当△ABC绕点C沿顺时针连续旋转五次后（如图3），得到一个正六边形。 它的六个角都等于120°，六条边分别相等。 评析：由于等边三角形的每个角等于60°，三条边分别相等，这两个特点有特殊性，可得出新的特殊图形。 【考点突破】 【考点指要】 由于图形旋转不改变它的形状和大小，因此连续绕某点旋转后，可以得出某些特殊图形，这样便把旋转与对图形的形状的判断结合起来，带有一定的综合性。在中考试题中，有可能出现；尤其是旋转后图形的计算或点的坐标的确定也常出现，应予以重视。 【典型例题分析】 例1. （2005年吉林）如图，A点坐标为（3，3），将△ABC先向下平移4个单位得△A'B'C'，再将△A'B'C'绕点O逆时针旋转180°得△A''B''C''。请你画出△A'B'C'和△A''B''C''，并写出点A''的坐标。 分析：△ABC向下平移4个单位，只要把A、B、C三点的纵坐标下移4个单位即可；而将△A'B'C'绕点O逆时针旋转180°，只要找到A'、B'、C'三点关于点O的对称点即可。 解：将A、B、C三点分别向下移动4个单 ... ...