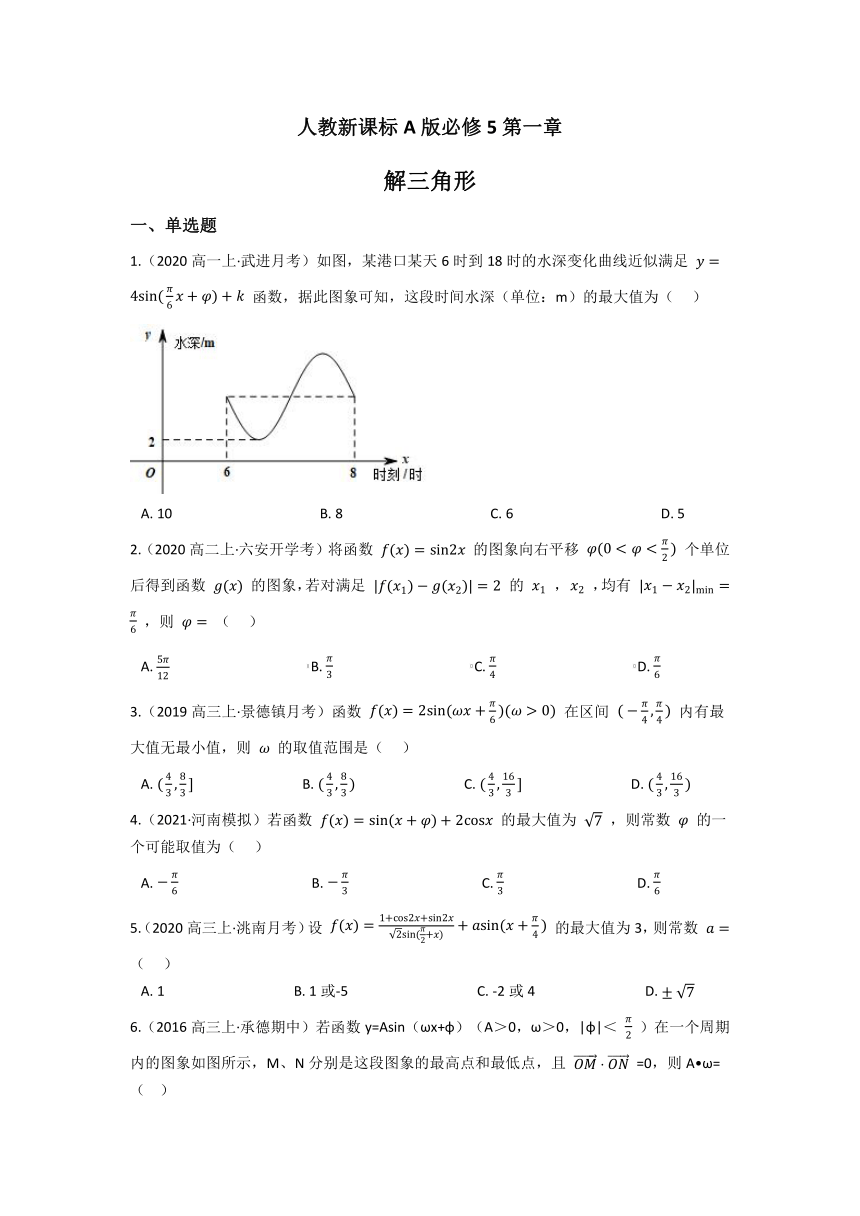
人教新课标A版必修5第一章 解三角形 一、单选题 1.(2020高一上·武进月考)如图,某港口某天6时到18时的水深变化曲线近似满足 函数,据此图象可知,这段时间水深(单位:m)的最大值为( ) A. 10 B. 8 C. 6 D. 5 2.(2020高二上·六安开学考)将函数 的图象向右平移 个单位后得到函数 的图象,若对满足 的 , ,均有 ,则 ( ) A. B. C. D. 3.(2019高三上·景德镇月考)函数 在区间 内有最大值无最小值,则 的取值范围是( ) A. B. C. D. 4.(2021·河南模拟)若函数 的最大值为 ,则常数 的一个可能取值为( ) A. B. C. D. 5.(2020高三上·洮南月考)设 的最大值为3,则常数 ( ) A. 1 B. 1或-5 C. -2或4 D. 6.(2016高三上·承德期中)若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< )在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且 =0,则A ω=( ) A. B. C. D. 7.(2021·青岛模拟)若将函数 的图象向左平移 个单位后得到的图象关于 轴对称,则函数 在 上的最大值为( ) A. 2 B. C. 1 D. 8.(2020高一下·洛阳期末)已知函数 ,当 时, 时,则 的值最多有( ) A. 4个 B. 3个 C. 2个 D. 1个 9.(2021高一下·石家庄期末)已知菱形 边长为1, ,对角线 与 交于点O,将菱形 沿对角线 折成平面角为 的二面角,若 ,则折后点O到直线 距离的最值为( ) A.最小值为 ,最大值为 B.最小值为 ,最大值为 C.最小值为 ,最大值为 D.最小值为 ,最大值为 二、填空题 10.(2020高一上·宁波期末)若函数 的最小值为1,则正实数 _____. 11.(2019高一下·顺德期末)在 中,两直角边和斜边分别为a,b,c,若 则实数x的取值范围是_____. 12.(2019高二上·浙江月考)已知函数 ,对任意的 ,存在实数 ,使得 成立,则实数a的最大值为_____. 13.(2019高一下·嘉定月考)已知 ,则 的取值范围为_____. 14.(2020高一上·芜湖期末)当 时.函数 取得最大值,则 . 15.(2020高三上·平阳月考)已知 ,若函数 的最大值为5,则 _____. 16.(2020高三上·天津期末)已知扇形 半径为 , ,弧 上的点 满足 ,则 的最大值是_____; 最小值是_____; 17.(2019高一下·安徽期中)如图,已知正方形 的边长为2,点 为 的中点.以 为圆心, 为半径,作弧交 于点 .若 为劣弧 上的动点,则 的最小值为_____. 三、解答题 18.(2020高一上·绍兴期末)已知函数 . (1)求 的值; (2)若 ,求 的值域. 19.(2020高一上·东丽期末)已知函数 的最大值为1 (1)求常数m的值; (2)当 时,求函数 的单调递增区间. 20.(2020高一上·福建期末)已知函数 . (Ⅰ)求 的最小正周期及对称轴方程; (Ⅱ)当 时,求函数 的最大值、最小值,并分别求出使该函数取得最大值、最小值时的自变量 的值. 21.(2019高三上·昌吉月考)已知函数 . (1)求函数 的最小正周期及最大值时x取值; (2)令 ,判断函数 的奇偶性,并说明理由. 答案解析部分 一、单选题 1.【答案】 A 【解析】某港口某天6时到18时的水深变化曲线近似满足函数 , 据此图象可知,这段时间水深最小值为 ,所以 , 故这段时间水深的最大值为 , 故答案为:A. 2.【答案】 B 【解析】由题意可得: , 由 可知,两个函数的最大值与最小值的差等于2,有 , 不妨取 ,则 ,即 在 取得最小值, 所以 ,此时 ,符合题意, 取 ,则 ,即 在 取得最大值, 所以 ,此时 ,满足题意,所以 故答案为:B 3.【答案】 A 【解析】解:当 时, 令 ,解得 , 当 时, 可取最大值, 令 ,解得 , 当 时, 可取最小值, 与函数 在区间 内有最大值无最小值矛盾,故 ,排除CD; 当 时, 令 ,解得 , 当 时, 可取最大值, 令 ,解得 , 不存在 ,使 , 故 时,函数 在区间 内有最大值 ... ...
~~ 您好,已阅读到文档的结尾了 ~~