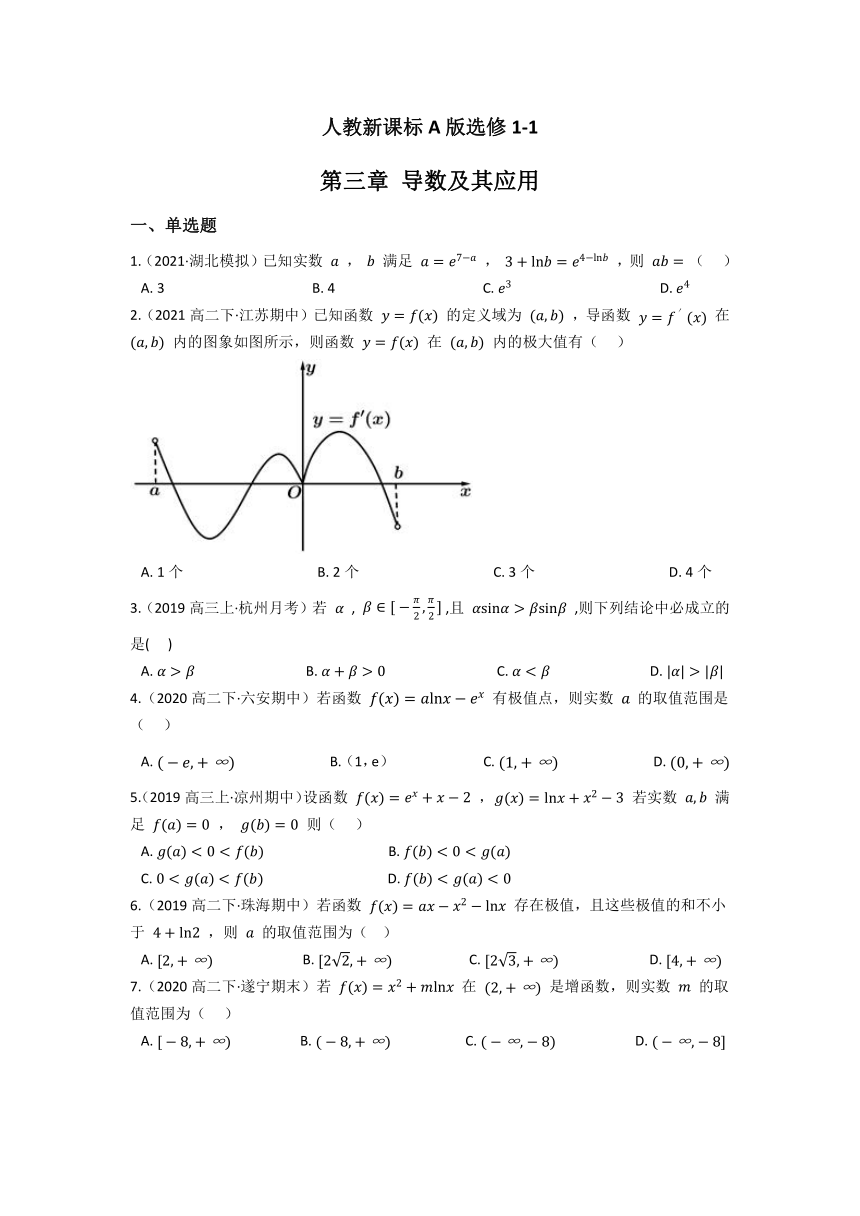
人教新课标A版选修1-1 第三章 导数及其应用 一、单选题 1.(2021·湖北模拟)已知实数 , 满足 , ,则 ( ) A. 3 B. 4 C. D. 2.(2021高二下·江苏期中)已知函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内的极大值有( ) A. 1个 B. 2个 C. 3个 D. 4个 3.(2019高三上·杭州月考)若 , ,且 ,则下列结论中必成立的是( ) A. B. C. D. 4.(2020高二下·六安期中)若函数 有极值点,则实数 的取值范围是( ) A. B. (1,e) C. D. 5.(2019高三上·凉州期中)设函数 , 若实数 满足 , 则( ) A. B. C. D. 6.(2019高二下·珠海期中)若函数 存在极值,且这些极值的和不小于 ,则 的取值范围为( ) A. B. C. D. 7.(2020高二下·遂宁期末)若 在 是增函数,则实数 的取值范围为( ) A. B. C. D. 8.(2021·常德模拟)已知函数 ,若函数 恰有5个零点,则实数 的取值范围是( ) A. B. C. D. 9.(2019高二下·衢州期中)设函数 是定义在 上的可导函数,其导函数为 ,且有 ,则不等式 的解集为( ) A. B. C. D. 10.(2020高三上·杭州期中)已知函数 ,若恰有3个互不相同的实数 , , ,使得 ,则实数 的取值范围为( ) A. B. C. D. 或 11.(2019高二下·奉化期末)若函数 至少存在一个零点,则m的取值范围为( ) A. B. C. D. 二、填空题 12.(2019高三上·深州月考)曲线y=x2+lnx在点(1,1)处的切线方程为 _____. 13.(2020高二下·广州期末)若函数 ( 是自然对数的底数)在 的定义域上单调递增,则称函数 具有M性质.下列函数中所有具有M性质的函数的序号为_____. ① ② ③ ④ 14.(2020高二下·滨海新月考)函数 的定义域为 ,导函数 在 内的图象如图所示,则函数 在 内有极小值点的个数为_____. 15.(2020高三上·清新月考)法国数学家拉格朗日于1778年在其著作《解析函数论》中提出一个定理:如果函数 满足如下条件: ⑴在闭区间 上是连续不断的; ⑵在区间 上都有导数. 则在区间 上至少存在一个数 ,使得 ,其中 称为拉格朗日中值.则 在区间 上的拉格朗日中值 _____. 16.(2019高三上·武汉月考)如图,圆形纸片的圆心为 ,半径为 ,该纸片上的正方形 的中心为 , 、 、 、 为圆 上点, , , , 分别是以 , , , 为底边的等腰三角形,沿虚线剪开后,分别以 , , , 为折痕折起 , , , ,使得 、 、 、 重合,得到四棱锥.当该四棱锥体积取得最大值时,正方形 的边长为_____ . 17.(2020高三上·兴宁期末)函数 在 上不单调,则实数a的取值范围是_____. 18.(2019高二下·双鸭山月考)对于任意的实数 ,总存在三个不同的实数 ,使得 成立,则实数 的取值范围为_____ 19.(2021高三上·辽宁月考)已知函数 满足 恒成立,则实数 的取值范围是 . 20.(2019高二下·安徽期中)如图,有一矩形钢板ABCD缺损了一角(如图所示),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1m,AD=0.5m,则五边形ABCEF的面积最大值为_____m2. 三、解答题 21.(2020高二下·潍坊期末)已知函数 ,其中 . (1)当 时,求曲线 在点 处的切线方程; (2)求函数 的单调区间与极值. 22.(2020高二下·海安月考)已知 ( 且m为常数). (1)讨论函数 的单调性; (2)若对任意的 ,都存在 ,使得 (其中e为自然对数的底数),求实数k的取值范围. 23.(2021高二下·淄博期末)已知函数 ,其中 是自然对数的底数. (1)判断函数 在区间 上的单调性,并求最小值; (2)设 ,证明:函数 在区间 上有唯一零点. 24.(2020高三上·枣庄月考)设函数 . (1)若当 时, 取得极值,求 的值,并讨论 的单调性; (2)若 存在极值,求 的取值范围,并证 ... ...
~~ 您好,已阅读到文档的结尾了 ~~