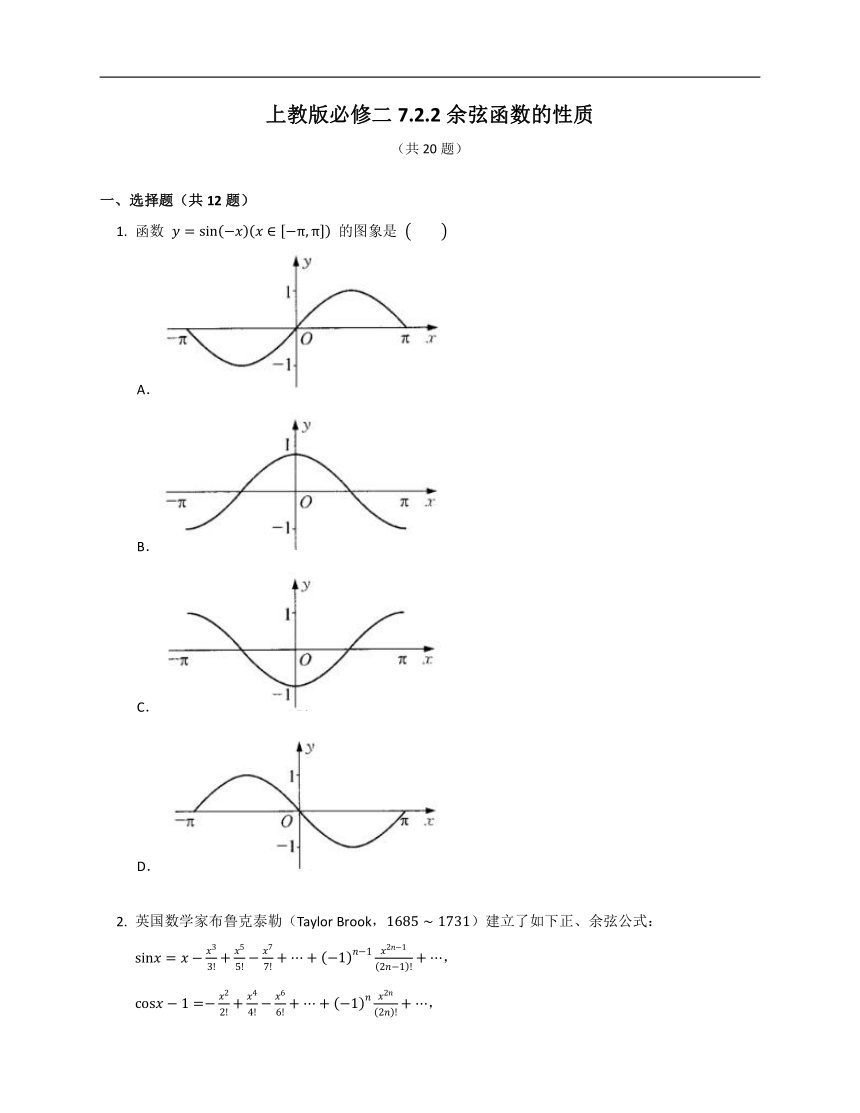
上教版必修二7.2.2余弦函数的性质 (共20题) 一、选择题(共12题) 函数 的图象是 A. B. C. D. 英国数学家布鲁克泰勒(Taylor Brook,)建立了如下正、余弦公式: , , 其中 ,,,例如:,,. 试用上述公式估计 的近似值为(精确到 ) A. B. C. D. 已知角 , 是 中的两个内角,则“”是“”的 A.充分不必要条件 B.必要不充分条件 C.既不充分也不必要条件 D.充要条件 函数 是 A.奇函数,且最大值为 B.偶函数,且最大值为 C.奇函数,且最大值为 D.偶函数,且最大值为 在三角形 中,角 ,, 成等差数列,则 的大小为 A. B. C. D. 若 ,则使 和 同时成立的 的取值范围是 A. B. C. D. “”是“”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 函数 的图象大致为 A. B. C. D. 在锐角 中,若 ,则 的范围 A. B. C. D. 使 取最小值的 的集合是 A. B. C. D. 下列函数中,最小正周期为 的是 A. B. C. D. 若 ,则实数 的取值范围是 A. B. C. D. 二、填空题(共4题) 设 , 都是锐角,,.请问 是否可以求解,若能求解,求出答案;若不能求解,简述理由: . 函数 的单调递增区间为 . 函数 的定义域为 . 函数 的最小值为 . 三、解答题(共4题) 比较下列函数值的大小. (1) 与 ; (2) 与 ; (3) 与 ; (4) 与 . 设 , 为常数,,,且 为偶函数. (1) 求 的值. (2) 若 的最小值为 ,且 ,求 的值. 已知 ,求函数 的最小正周期. 已知 . (1) 求函数 的值域; (2) 求函数 的值域. 答案 一、选择题(共12题) 1. 【答案】D 2. 【答案】B 【解析】由题设中的余弦公式得 3. 【答案】D 【解析】当“”时,由于 , 在 上为减函数,故“”. 当“”时,由于 , 在 上为减函数,可得到“”.故为充要条件.故选D. 4. 【答案】D 【解析】由题意,,所以该函数为偶函数, 又 , 所以当 时, 取最大值 . 故选:D. 5. 【答案】B 【解析】因为在三角形 中,角 ,, 成等差数列,所以 ,, 可得 , 所以 . 6. 【答案】D 7. 【答案】B 8. 【答案】C 【解析】函数 ,当 时,是函数的一个零点,属于排除A,B; 当 时,,,函数 ,函数的图象在 轴下方,排除D. 9. 【答案】A 【解析】由正弦定理得 , 因为 是锐角三角形, 所以三个内角均为锐角, 即有 ,,, 解得 , 又余弦函数在此范围内是减函数,故 . 所以 . 10. 【答案】A 11. 【答案】C 【解析】作出 和 的图象(图略),可知 的最小正周期为 , 的最小正周期为 ,从而 与 的最小正周期分别为 和 ,故选C. 12. 【答案】A 【解析】因为 , 所以 ,于是 , 解得 . 二、填空题(共4题) 13. 【答案】 ,,因为 在 上单调递减,而 .所以条件有误,不可解 14. 【答案】 , 【解析】因为对数的真数大于零, 所以 ,, 解之得函数的定义域为:,, 令 , 因为 , 所以 关于 的单调减区间是函数 的单调递增区间, 由 ,,得 ,, 再结合函数的定义域,得 ,是原函数的增区间. 15. 【答案】 , 16. 【答案】 【解析】因为 , 令 ,则 , 所以 . 又函数 图象的对称轴 ,且开口向下, 所以当 时, 有最小值 . 综上, 的最小值为 . 三、解答题(共4题) 17. 【答案】 (1) 因为 ,且 在 上单调递增,所以 . (2) , , 因为 ,且 在 上单调递减, 所以 ,即 . (3) 因为 ,, 又因为 ,且 在 上单调递减, 所以 ,即 . (4) 因为 ,且 , 在 上单调递增, 所以 ,即 . 18. 【答案】 (1) 因为 为偶函数, 所以 恒成立, 即 恒成立, 所以 恒成立, 所以 . (2) 的最小值是 , 所以 , 所以 ,, 又 ,, 故舍去 , 所以 . 19. 【答案】因为 , 所以 . 所以最小正周期 . 20. 【答案】 (1) 因为 在 ... ...
~~ 您好,已阅读到文档的结尾了 ~~