4.3统计模型 作业（含解析）

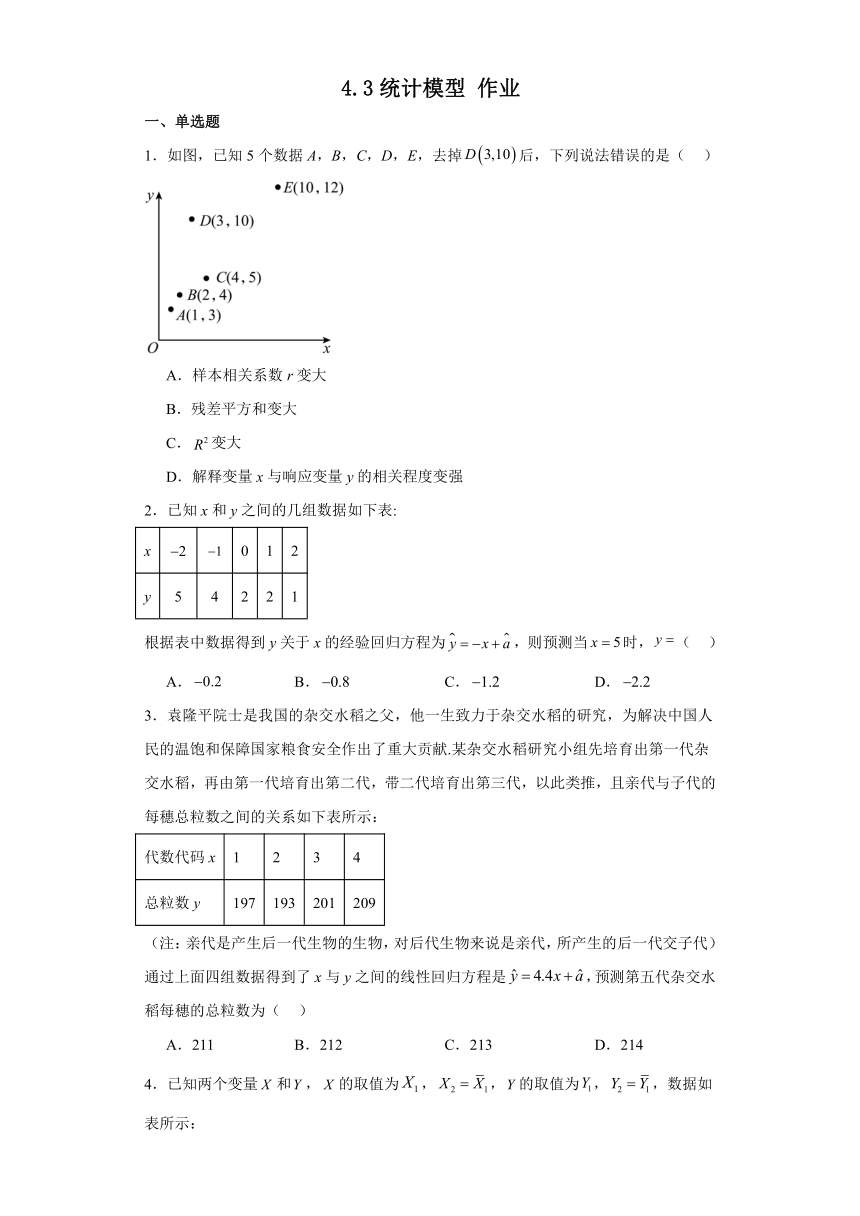
4.3统计模型 作业 一、单选题 1．如图，已知5个数据A，B，C，D，E，去掉后，下列说法错误的是（ ） A．样本相关系数r变大 B．残差平方和变大 C．变大 D．解释变量x与响应变量y的相关程度变强 2．已知x和y之间的几组数据如下表: x 0 1 2 y 5 4 2 2 1 根据表中数据得到y关于x的经验回归方程为，则预测当时，（ ） A． B． C． D． 3．袁隆平院士是我国的杂交水稻之父，他一生致力于杂交水稻的研究，为解决中国人民的温饱和保障国家粮食安全作出了重大贡献.某杂交水稻研究小组先培育出第一代杂交水稻，再由第一代培育出第二代，带二代培育出第三代，以此类推，且亲代与子代的每穗总粒数之间的关系如下表所示： 代数代码x 1 2 3 4 总粒数y 197 193 201 209 （注：亲代是产生后一代生物的生物，对后代生物来说是亲代，所产生的后一代交子代）通过上面四组数据得到了x与y之间的线性回归方程是，预测第五代杂交水稻每穗的总粒数为（ ） A．211 B．212 C．213 D．214 4．已知两个变量和，的取值为，，的取值为，，数据如表所示： 总计 总计 以下数据能说明与有关联的可能性最大的一组为（ ） A．，，， B．，，， C．，，， D．，，， 5．某地政府调查育龄妇女生育意愿与家庭年收入高低的关系时，随机调查了当地3000名育龄妇女，用独立性检验的方法处理数据，并计算得，则根据这一数据以及临界值表，判断育龄妇女生育意愿与家庭年收入高低有关系的可信度（ ） 参考数据如下：，. A．低于 B．低于 C．高于 D．高于 6．两个变量与的回归模型中，分别选择了个不同模型，它们对应的的值如下，其中拟合效果最好的模型是（ ） A．模型对应的 B．模型对应的 C．模型对应的 D．模型对应的 7．通过随机询问某中学110名中学生是否爱好跳绳，得到如下列联表： 跳绳 性别 合计 男 女 爱好 40 20 60 不爱好 20 30 50 合计 60 50 110 已知， 0.05 0.01 0.001 3.841 6.635 10.828 则以下结论正确的是（ ） A．根据小概率值的独立性检验，爱好跳绳与性别无关 B．根据小概率值的独立性检验，爱好跳绳与性别无关，这个结论犯错误的概率不超过0.001 C．根据小概率值的独立性检验，有99%以上的把握认为“爱好跳绳与性别无关” D．根据小概率值的独立性检验，在犯错误的概率不超过1%的前提下，认为“爱好跳绳与性别无关” 8．根据分类变量与的成对样本数据，计算得到．已知，则依据小概率值的独立性检验，可以推断变量与（ ） A．独立，此推断犯错误的概率是 B．不独立，此推断犯错误的概率是 C．独立，此推断犯错误的概率不超过 D．不独立，此推断犯错误的概率不超过 二、多选题 9．为了解阅读量多少与幸福感强弱之间的关系，一个调查机构根据所得到的数据，绘制了如下的2×2列联表（个别数据暂用字母表示）： 单位：人 阅读量 幸福感 合计 幸福感强 幸福感弱 阅读量多 m 18 72 阅读量少 36 n 78 合计 90 60 150 计算得，对于下面的选项，正确的为（ ） A． B． C．根据小概率值的独立性检验，可以认为“阅读量多少与幸福感强弱无关” D．根据小概率值的独立性检验，可以在犯错误的概率不超过0.005的前提下认为“阅读量多少与幸福感强弱有关” 10．下列说法中，正确的命题是（ ） A．对于任意两个事件与，如果，则事件与独立 B．已知两个变量具有线性相关关系，其回归直线方程为，若，，，则 C．， D．随机变量服从正态分布，若，则 11．如图所示是某市2022年4月至2023年3月每月最低气温与最高气温的折线统计图，已知每月最低气温与最高气温的样本相关系数，则下列结论正确的是（若，则线性相关程度较强）（ ） A．每月最低气温与最高气温有较强的线性相关性，且二者为正线性相关 B．月温差（月最高气温一月最低气温）的最大值出现在10月 C．9~12月的月温差 ... ...