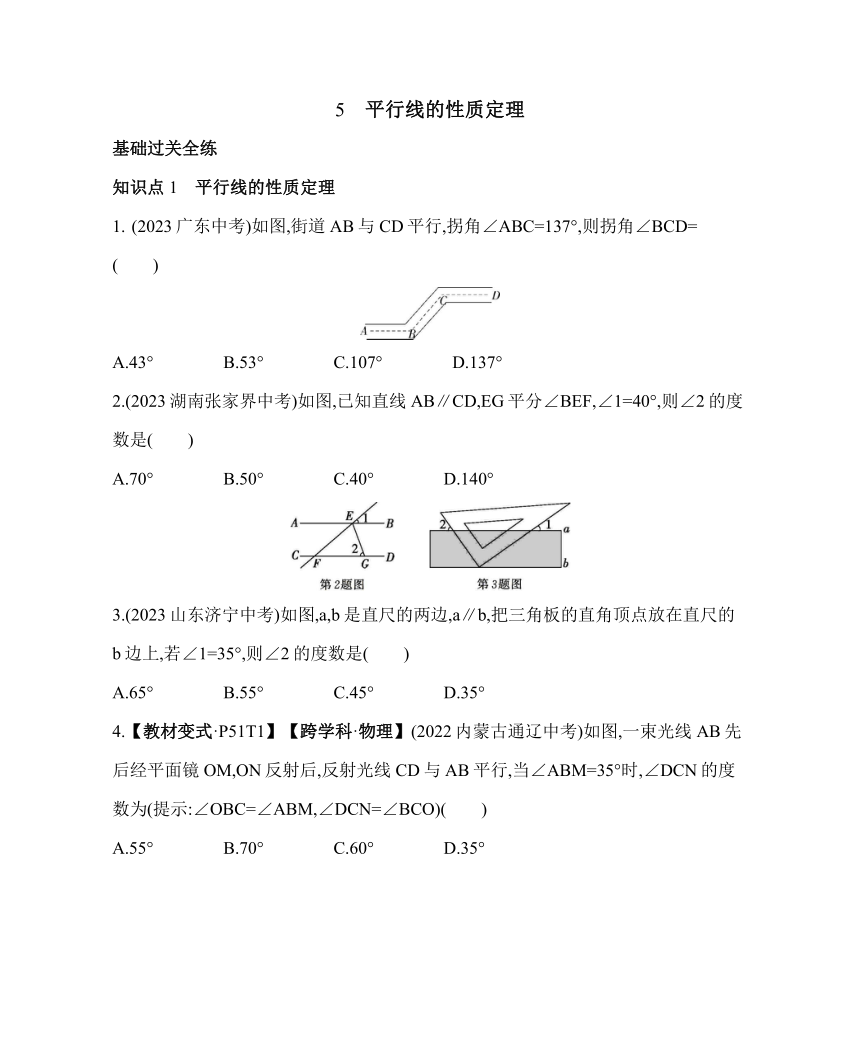
5 平行线的性质定理 基础过关全练 知识点1 平行线的性质定理 (2023广东中考)如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD= ( ) A.43° B.53° C.107° D.137° 2.(2023湖南张家界中考)如图,已知直线AB∥CD,EG平分∠BEF,∠1=40°,则∠2的度数是( ) A.70° B.50° C.40° D.140° 3.(2023山东济宁中考)如图,a,b是直尺的两边,a∥b,把三角板的直角顶点放在直尺的b边上,若∠1=35°,则∠2的度数是( ) A.65° B.55° C.45° D.35° 4.【教材变式·P51T1】【跨学科·物理】(2022内蒙古通辽中考)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为(提示:∠OBC=∠ABM,∠DCN=∠BCO)( ) A.55° B.70° C.60° D.35° 5.【一题多变·已知三直线平行,求角的关系】(2022山东聊城临清二模)如图,若AB∥CD∥EF,则∠BCE=( ) A.180°-∠2+∠1 B.180°-∠1-∠2 C.∠2-2∠1 D.∠1+∠2 [变式1·已知三直线平行,求角的度数和]如图,如果AB∥CD∥EF,那么∠BAC+ ∠ACE+∠CEF=( ) A.180° B.270° C.360° D.540° [变式2·已知三直线平行及角的度数和,求另一个角的度数]如图,直线AB∥CD∥EF,如果∠A+∠ADF=208°,那么∠F= . 如图,把一张对边互相平行的纸条沿EF折叠,若∠EFB=32°,则下列结论: ①∠C'EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°. 其中正确的有 个. 7.如图,AB∥CD,BC∥DE,∠D=110°,求∠B的度数. 8.我们生活中经常接触的小刀的示意图如图所示,小刀由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,则∠1与∠2的度数和是一个定值吗 若是,请求出∠1与∠2的度数和;若不是,请说明理由. 知识点2 平行线的性质定理与判定定理的关系 9.(2023山东济宁微山三模)如图,已知∠1=∠2=50°,∠3=60°,则∠4等于( ) A.50° B.60° C.70° D.120° 10.(2022湖北武汉中考)如图,在四边形ABCD中,AD∥BC,∠B=80°. (1)求∠BAD的度数; (2)AE平分∠BAD交BC于点E,∠BCD=50°.求证:AE∥DC. 能力提升全练 11.(2023山东东营中考,3,★)如图,AB∥CD,点E在线段BC上(不与点B,C重合),连接DE.若∠D=40°,∠BED=60°,则∠B=( ) A.10° B.20° C.40° D.60° 12.(2023山东菏泽中考,3,★)一把直尺和一个含30°角的直角三角板按如图所示的方式放置,若∠1=20°,则∠2=( ) A.30° B.40° C.50° D.60° 13.(2023浙江金华中考,7,★★)如图,已知∠1=∠2=∠3=50°,则∠4的度数是( ) A.120° B.125° C.130° D.135° 14.(2023山东济南中考,3,★★)如图,一块直角三角板的直角顶点放在直尺的一边上.如果∠1=70°,那么∠2的度数是( ) A.20° B.25° C.30° D.45° 15.【跨学科·物理】(2022山东潍坊中考,5,★★)小亮绘制的潜望镜原理示意图如图所示,两个平面镜的镜面AB与CD平行,入射光线l与反射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为(提示:∠2=∠1,∠4=∠3)( ) A.100°40' B.100°20' C.99°40' D.99°20' 16.【新考法】(2023山东烟台中考,12,★)一杆古秤在称物时的状态如图所示,已知∠1=102°,则∠2的度数为 . (2022山东滨州滨城月考,18,★★)如图,已知∠A=∠AGE,∠D=∠1,且∠1+∠2 =180°,则下列结论:①CE∥BF,②∠A=∠D,③AB∥CD,④∠C=∠B.其中正确的结论是 .(只填序号) 18.(2023山东济南莱 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

