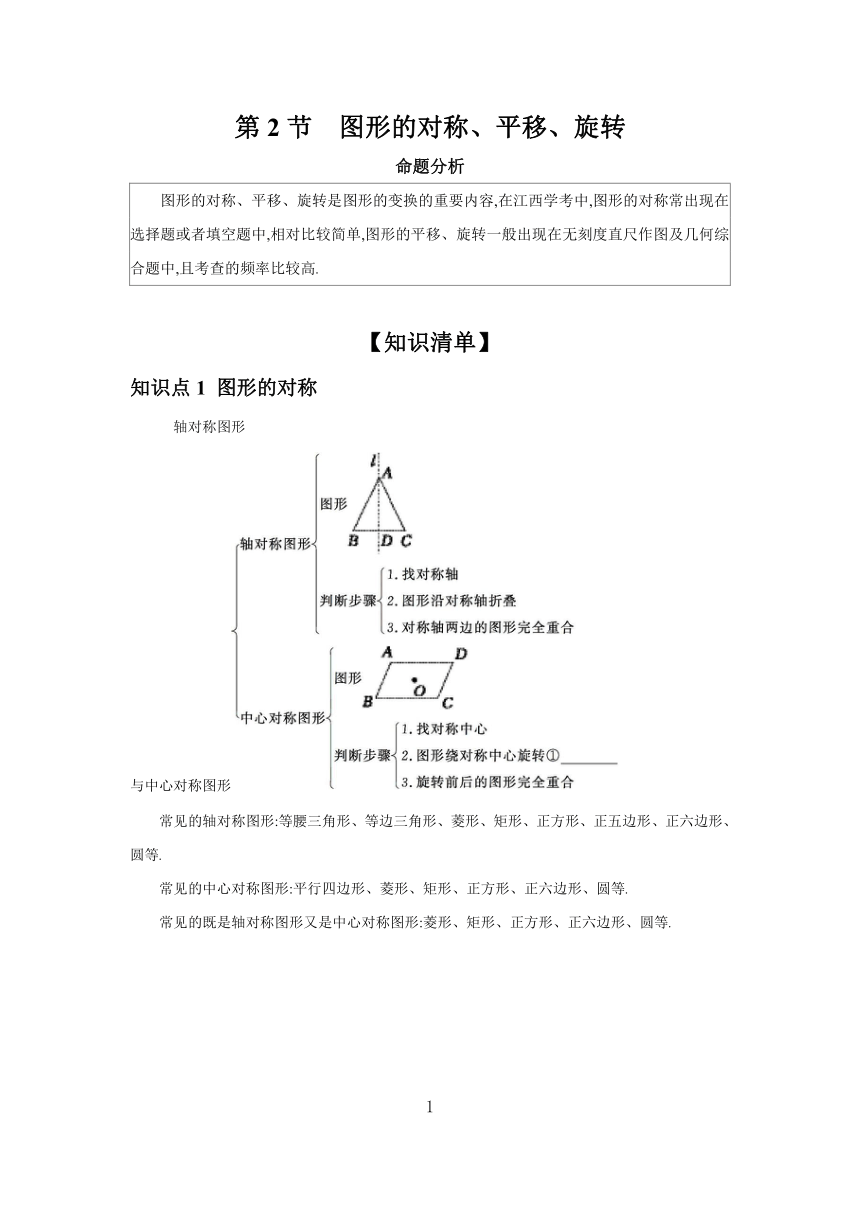
第2节 图形的对称、平移、旋转 命题分析 图形的对称、平移、旋转是图形的变换的重要内容,在江西学考中,图形的对称常出现在选择题或者填空题中,相对比较简单,图形的平移、旋转一般出现在无刻度直尺作图及几何综合题中,且考查的频率比较高. 【知识清单】 知识点1 图形的对称 轴对称图形 与中心对称图形 常见的轴对称图形:等腰三角形、等边三角形、菱形、矩形、正方形、正五边形、正六边形、圆等. 常见的中心对称图形:平行四边形、菱形、矩形、正方形、正六边形、圆等. 常见的既是轴对称图形又是中心对称图形:菱形、矩形、正方形、正六边形、圆等. 轴对称 与中心对称 知识点2 图形的折叠 图形的折叠 知识点3 平移与旋转 内容 要素 性质 作图步骤 (1)平移的方向; (2)平移的距离 (1)平移前后对应线段平行(或共线)且⑤ ,对应点所连的线段⑥ ; (2)对应角分别⑦ ,且对应角的两边分别平行(或共线),方向一致; (3)平移变换后的图形与原图形⑧ (1)确定平移方向和平移距离; (2)找原图形的关键点; (3)按平移方向和平移距离各关键点; (4)按原图形顺次连接各关键点平移后的对应点,得到平移后的图形 (1)旋转中心; (2)旋转方向; (3)旋转角度 (1)对应点到旋转中心的距离⑨ (2)对应点与旋转中心所连线段的夹角等于⑩ (3)旋转前后的图形 (1)确定旋转中心、旋转方向及旋转角; (2)找原图形的关键点; (3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点; (4)按原图形顺次连接各关键点旋转后的对应点,得到旋转后的图形 知识点4 图形的位似 图形的位似 【参考答案】 ①180° ②垂直平分 ③全等 ④相等 ⑤相等 ⑥平行且相等 ⑦相等 ⑧全等 ⑨相等 ⑩旋转角 全等 【自我诊断】 1.(文化自信)中国传统文化博大精深.下面四个图形中既是轴对称图形又是中心对称图形的是 ( ) A B C D 2. 如图,将四边形ABCD沿BC方向平移后得到四边形PEFQ,若BF=8,CE=4,则平移的距离为 ( ) A.2 B.3 C.4 D.5 3.如图,Rt△ABC向右翻滚,下列说法正确的有 ( ) (1)① ②是旋转; (2)① ③是平移; (3)① ④是平移; (4)② ③是旋转. A.1个 B.2个 C.3个 D.4个 4.如图,在平面直角坐标系中,点A的坐标为(-1,),以原点O为中心,将点A顺时针旋转90°得到点A',则点A'坐标为 ( ) A.(1,-) B.(-,1) C.(0,2) D.(,1) 5.如图,在Rt△ABC中,∠ACB=90°,∠B=70°,将Rt△ABC绕点C顺时针旋转角度α(0°<α<180°)得到Rt△A1B1C,使得A1,B1,A三点共线,则α的度数为 ( ) A.110° B.120° C.130° D.140° 【参考答案】 1.C 2.A 3.C 4.D 5.D 【真题精粹】 考向1 对称图形的判断 1.(2023·江西)下列图形中,是中心对称图形的是 ( ) A B C D 2.(拓展)下列图形中,是轴对称图形的是 ( ) A B C D 考向2 对称图形的相关计算 3.(2019·江西)如图,在△ABC中,D是BC上的点,∠BAD=∠ABC=40°,将△ABD沿着AD翻折得到△AED,则∠CDE= . 4.(拓展)如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标. (2)写出顶点B,C,B1,C1的坐标. 考向3 图形的平移 5.(2018·江西)小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有 ( ) A.3个 B.4个 C.5个 D.无数个 6.(拓展)如图,把△ABC(点A,B,C均在网格格点处)的顶点A先向下平移2格,再向左平移1格到达A'点,连接A'B,则线段A'B与线段AC的关系是 ( ) A.相等 B.平分 C.垂直 D.平分且垂直 考向4 图形的旋转 类型1 与旋转有关的计算 7.如图, 在△ABC中,∠BAC=33°, ... ...
~~ 您好,已阅读到文档的结尾了 ~~