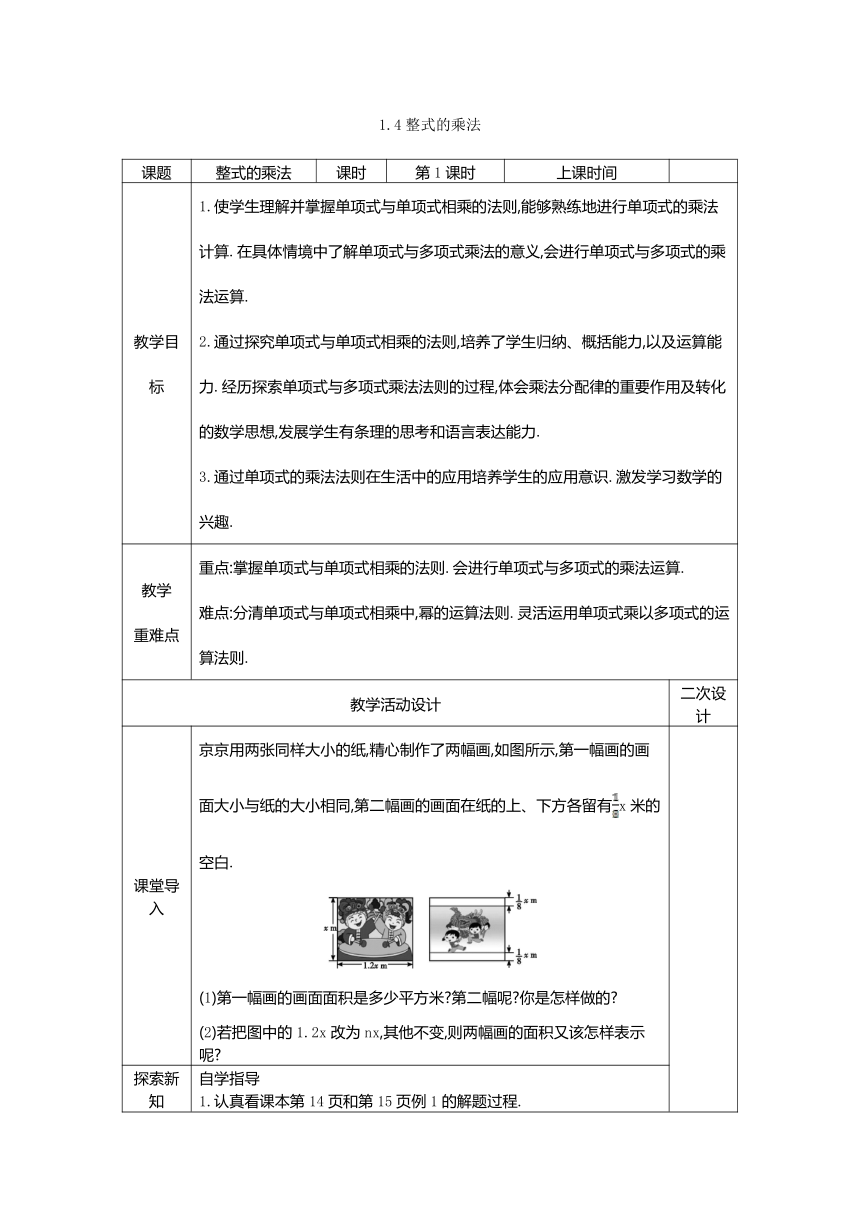
1.4整式的乘法 课题 整式的乘法 课时 第1课时 上课时间 教学目标 1.使学生理解并掌握单项式与单项式相乘的法则,能够熟练地进行单项式的乘法计算.在具体情境中了解单项式与多项式乘法的意义,会进行单项式与多项式的乘法运算. 2.通过探究单项式与单项式相乘的法则,培养了学生归纳、概括能力,以及运算能力.经历探索单项式与多项式乘法法则的过程,体会乘法分配律的重要作用及转化的数学思想,发展学生有条理的思考和语言表达能力. 3.通过单项式的乘法法则在生活中的应用培养学生的应用意识.激发学习数学的兴趣. 教学 重难点 重点:掌握单项式与单项式相乘的法则.会进行单项式与多项式的乘法运算. 难点:分清单项式与单项式相乘中,幂的运算法则.灵活运用单项式乘以多项式的运算法则. 教学活动设计 二次设计 课堂导入 京京用两张同样大小的纸,精心制作了两幅画,如图所示,第一幅画的画面大小与纸的大小相同,第二幅画的画面在纸的上、下方各留有x米的空白. (1)第一幅画的画面面积是多少平方米 第二幅呢 你是怎样做的 (2)若把图中的1.2x改为nx,其他不变,则两幅画的面积又该怎样表示呢 探索新知 合作探究 自学指导 1.认真看课本第14页和第15页例1的解题过程. 2.注意单项式与单项式相乘中系数与相同字母的幂分别相乘的过程. 3.注意例题的思路、步骤和格式. 如有问题,可小声与同桌讨论,或举手问老师.5分钟后,比比谁能正确的完成自我检测题. 合作探究 继续引导学生分析实例中出现的算式,教师提出以下三个问题: 问题1:对于课堂导入实际问题的结果x·nx,(nx)·x可以表达得更简单些吗 说说你的理由 问题2:类似地,3a2b·2ab3和(xyz)·y2z可以表达的更简单一些吗 问题3:如何进行单项式与单项式相乘的运算 归纳结论:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式. 问题4:在你探索单项式乘法运算法则的过程中,运用了哪些运算律和运算法则 学生回答:运用了乘法的交换律、结合律和同底数幂乘法的运算性质. 【例1】计算: (1)(2xy2)·xy; (2)(-2a2b3)·(-3a); (3)(4×10)5×(5×104); 续表 探索新知 合作探究 (4)(-3a2b2)·(-a3b2)5; (5)-a2bc3·-c5·ab2c. 探究:宁宁作了一幅画,所用纸的大小如图所示,她在纸的左、右两边各留了x m的空白,这幅画的画面面积是多少 先让学生独立思考,之后全班交流.交流时引导学生呈现出自己的思考过程. 同学之中主要有两种做法: 法一:先表示出画面的长和宽,由此得到画面的面积为xmx-x; 法二:先求出纸的面积,再减去两块空白处的面积,由此得到画面的面积为mx2-x2. 教师启发学生:两种方法得到的答案不一样,到底哪种方法对 短暂的思考之后,学生回答都对,由此引出xmx-x=mx2-x2这个等式. 引导学生观察这个算式,并思考两个问题: 式子的左边是什么运算 能不能用学过的法则说明这个等式成立的原因 学生不难总结出:式子的左边是一个单项式与一个多项式相乘,利用乘法分配律可得xmx-x=x·mx-x·x,再根据单项式乘单项式法则或同底数幂的乘法性质得到x·mx-x·x=mx2-x2,即xmx-x=mx2-x2. 想一想: 问题1:ab·(abc+2x)及c2(m+n-p)等于什么 你是怎样计算的 问题2:如何进行单项式与多项式相乘的运算 【例2】 计算: (1)2ab(5a2b+3ab2); (2)ab2-2ab·ab; (3)(-2a)(2a2-3a+1); (4)(-12xy2-10x2y+21y3)(-6xy3). 续表 探索新知 合作探究 教师指导 1.易错点 (1)单项式 ①进行单项式乘法,应先确定结果的符号,再把同底数幂分别相乘,这时容易出现的错误是将系数相乘与相同字母指数相加混淆. ②不要遗漏只在一个单项式中出现的字母,要将其连同它的指数作为积的一个因式. ③单项式乘法法则对于三个以上的单项式相乘同样适用. ④单项式乘以单项式,结果仍为单项式. (2)单项式乘多项式 ①单项式乘多项式的积 ... ...
~~ 您好,已阅读到文档的结尾了 ~~