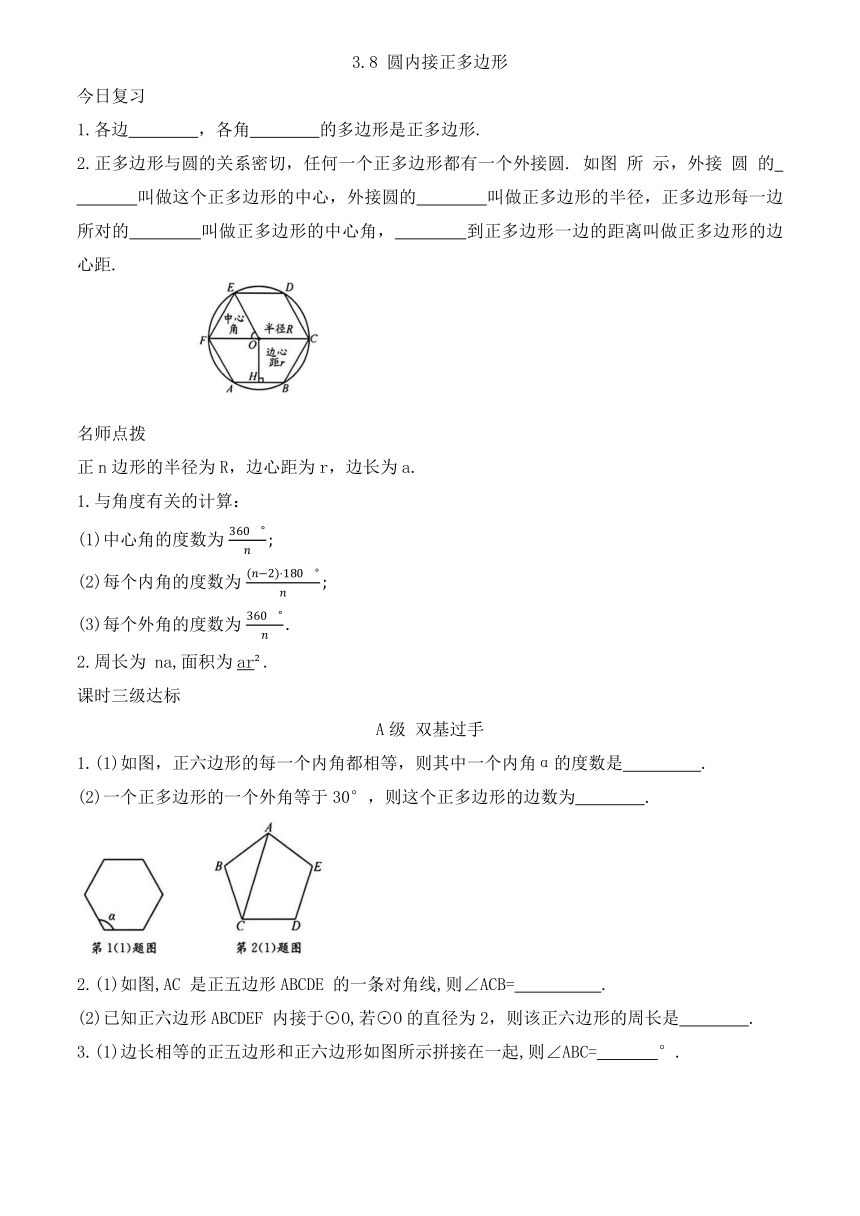
3.8 圆内接正多边形 今日复习 1.各边 ,各角 的多边形是正多边形. 2.正多边形与圆的关系密切,任何一个正多边形都有一个外接圆. 如图 所 示,外接 圆 的 叫做这个正多边形的中心,外接圆的 叫做正多边形的半径,正多边形每一边所对的 叫做正多边形的中心角, 到正多边形一边的距离叫做正多边形的边心距. 名师点拨 正n边形的半径为R,边心距为r,边长为a. 1.与角度有关的计算: (1)中心角的度数为 (2)每个内角的度数为 (3)每个外角的度数为 2.周长为 na,面积为ar . 课时三级达标 A级 双基过手 1.(1)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是 . (2)一个正多边形的一个外角等于30°,则这个正多边形的边数为 . 2.(1)如图,AC 是正五边形ABCDE 的一条对角线,则∠ACB= . (2)已知正六边形ABCDEF 内接于⊙O,若⊙O的直径为2,则该正六边形的周长是 . 3.(1)边长相等的正五边形和正六边形如图所示拼接在一起,则∠ABC= °. (2)如图,将正六边形 ABCDEF 放在直角坐标系中,中心与坐标原点重合.若点 A的坐标为(-1,0),则 点C的坐标为 . 4.(1)如图,正八边形 ABCDEFGH 内接于⊙O,若AC=4,则点 O到AC 的距离为 . (2)为增加绿化面积,某小区将原来的正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域.设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为 . 5.已知一个正六边形的边心距 ,则它的接圆的面积为 ( ) A.4π B.3π C.2π D.π 6.如图,在正六边形ABCDEF中,连接BF,BE,则关于△ABF外心的位置,下列说法正确的是( ) C A. 在△ABF内 B. 在△BFE内 C. 在线段 BF上 D. 在线段 BE上 7.如图,图中正方形ABCD 的边长为4,则图中阴影部分的面积为 ( ) A.16-4π B.32-8π C.8π-16 D. 无法确定 8.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF 的中心O 重合,且与边 AB,CD相交于点G,H(如图).图中阴影部分的面积记为S,三条线段GB,BC,CH的长度之和记为l,在大正六边形绕点O旋转过程中,下列说法正确的是( ) A. S变化,l不变 B. S不变,l变化 C. S变化,l变化 D. S与l均不变 9.(1)如图,AB,BC和AC 分别为⊙O内接正方形、正六边形和正n边形的一边,求n的值. (2)如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,求FG的长. 10.(1)如图,边长为 的正方形,剪去四个角后成为一个正八边形,求这个正八边形的边长. (2)如图,在 中, 点C,D 在 FG 上,且 ,过点A,C,D的⊙O分别交AF,AG于点B,E.求证:五边形ABCDE 是正五边形. B级 能力提升 11.如图,⊙O 与正八边形OABCDEFG 的边OA,OG分别交于点M,N,则MN所对的圆周角∠MPN的大小为 . 12.如图,已知正六边形 ABCDEF 的边长为2,G,H分别是AF 和CD的中点,P 是GH 上的动点,连接AP,BP,则AP+BP 的值最小时,BP 与 HG 的夹角(锐角)度数为 . 13.如图,正方形ABCD 内接于⊙O,E 为BC上一点,连接 BE,CE,若∠CBE=15°,BE=3,则 BC的长为 . 14.(1)如图,O为正六边形ABCDEF 的对角线 FD上的一点, 求S正六边形ABCDEF的值. (2)如图,在矩形ABCD中, 4,点O为矩形ABCD 的中心,以点 D为圆心、1为半径作⊙D,P 为⊙D 上的一个动点,连接AP,PO和OA,求 面积的最大值. C级 综合拓展 15.如图,已知AC,BD为⊙O的两条直径,连接AB,BC, 于点 E,F 是半径OC 的中点,连接EF. (1)设⊙O的半径为1,若 求线段EF的长. (2)连接BF,DF,设OB 与EF 交于点 P. ①求证: ②若 求 的度数. ... ...
~~ 您好,已阅读到文档的结尾了 ~~