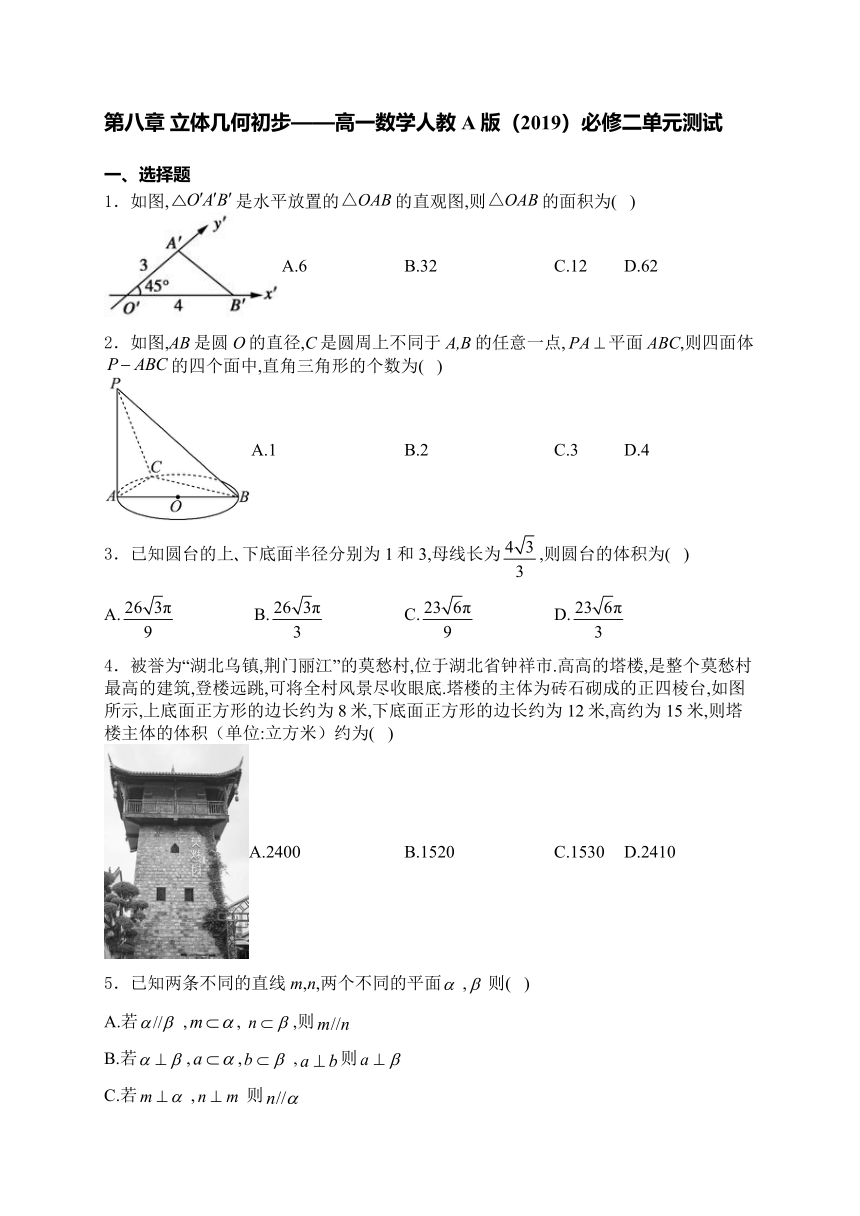
第八章 立体几何初步——高一数学人教A版（2019）必修二单元测试（含解析）

第八章 立体几何初步———高一数学人教A版（2019）必修二单元测试 一、选择题 1．如图,是水平放置的的直观图,则的面积为( ) A.6 B.32 C.12 D.62 2．如图,AB是圆O的直径,C是圆周上不同于A,B的任意一点,平面ABC,则四面体的四个面中,直角三角形的个数为( ) A.1 B.2 C.3 D.4 3．已知圆台的上 下底面半径分别为1和3,母线长为,则圆台的体积为( ) A. B. C. D. 4．被誉为“湖北乌镇,荆门丽江”的莫愁村,位于湖北省钟祥市.高高的塔楼,是整个莫愁村最高的建筑,登楼远跳,可将全村风景尽收眼底.塔楼的主体为砖石砌成的正四棱台,如图所示,上底面正方形的边长约为8米,下底面正方形的边长约为12米,高约为15米,则塔楼主体的体积（单位:立方米）约为( ) A.2400 B.1520 C.1530 D.2410 5．已知两条不同的直线m,n,两个不同的平面,则( ) A.若,,,则 B.若,,,则 C.若,则 D.若,,则 6．已知某圆锥的侧面积为,轴截面面积为1,则该圆锥的母线与底面所成的角为( ) A. B. C. D. 7．已知m是直线，，是两个不同的平面，下列正确的命题是( ) A.若，，则 B.若，，则 C.若，，则 D.若，，则 8．已知圆锥的底面半径是1，高为，则圆锥的侧面积是( ) A. B. C. D. 二、多项选择题 9．如图,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,则下列结论成立的是( ) A.平面PCD B.平面PDA C.平面PBA D.平面PBC 10．如图，正方体的棱长为1，动点P在对角线上，过P作垂直于的平面，记平面与正方体的截面多边形（含三角形）的周长为L，面积为S，，，下面关于函数和的描述正确的是( ) A.最大值为； B.在时取得极大值； C.在上单调递增，在上单调递减； D.在上单调递增，在上单调递减 11．如图,在棱长为2正方体中,E,F,G,H分别是,,CD,BC的中点,则下列说法正确的有( ) A.E,F,G,H四点共面 B.BD与EF所成角的大小为 C.在线段BD上存在点M,使得平面EFG D.在线段上任取一点N,三棱锥的体积为定值 三、填空题 12．在三棱锥中,,,D为AC的中点,平面ABC,且,则三棱锥外接球的表面积为_____. 13．已知m,n是两条不同的直线,、是两个不重合的平面,给出下列命题: ①若,,,则; ②若m,,,,则; ③是两条异面直线,若,,,,则. 上面的命题中,真命题的序号是_____.（写出所有真命题的序号） 14．如图，在棱长都相等的正三棱柱中，若P为棱的中点，则直线与直线所成的角为_____. 四、解答题 15．如图,在几何体中,平面平面ABCD,四边形ABCD为正方形,四边形为平行四边形,四边形为菱形,,,,E为棱的中点,点F在棱上,平面BDF. (1)证明平面ABCD； (2)求平面与平面BDF夹角的余弦值. 16．如图,在三棱柱中,,,分别是,的中点. (1)求证：平面 (2)若,求证：平面平面. 17．在正三棱柱中，M，O分别为，的中点. (1)证明：平面； (2)证明：平面. 18．如图,已知点P是平行四边形所在平面外的一点,E、F 分别是、上的点且E、F分别是、的中点.求证：平面. 19．已知三棱锥中,底面,,D,F分别为,的中点,于 E. (1)求证：平面; (2)求证：平面平面. 参考答案 1．答案：C 解析：由斜二测画法特点得, 为直角三角形, , 故选:C. 2．答案：D 解析：因为平面ABC,平面ABC,平面ABC,平面ABC 所以,,, 所以,为直角三角形, 又因为AB是圆O的直径,所以,为直角三角形 因为,平面PAC,平面PAC 所以平面PAC 又平面PAC, 所以,为直角三角形 综上,四面体的四个面都是直角三角形. 故选:D 3．答案：A 解析：因为圆台的上 下底面半径分别为1和3,母线长为, 所以圆台的高, 所以圆台的体积. 故选：A. 4．答案：B 解析：由题意,正四棱台的上底面边长约为8米,下底面边长约为12米,高约为15米, 可得正四棱台的上底面面积为64平方米,下底面面积为144平方米, 则塔楼主体的体积约为立方米. 故选:B. 5．答案：D 解析：对于A,若,,,则m,n可能平行,也可能异面,A错误; 对于B,若, ... ...