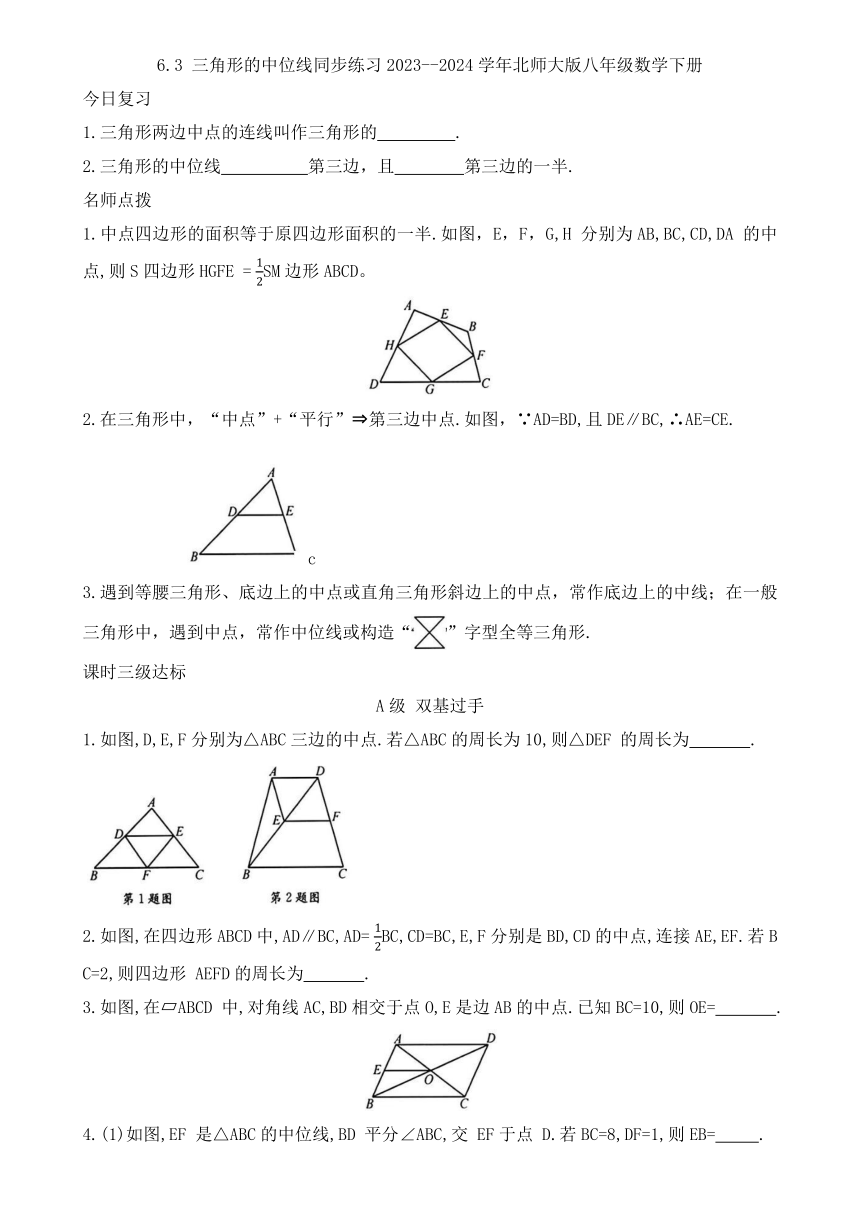
6.3 三角形的中位线同步分层训练(无答案)2023--2024学年北师大版八年级数学下册

6.3 三角形的中位线同步练习2023--2024学年北师大版八年级数学下册 今日复习 1.三角形两边中点的连线叫作三角形的 . 2.三角形的中位线 第三边，且 第三边的一半. 名师点拨 1.中点四边形的面积等于原四边形面积的一半.如图，E，F，G,H 分别为AB,BC,CD,DA 的中点,则S四边形HGFE = SM边形ABCD。 2.在三角形中，“中点”+“平行” 第三边中点.如图，∵AD=BD,且DE∥BC,∴AE=CE. c 3.遇到等腰三角形、底边上的中点或直角三角形斜边上的中点，常作底边上的中线；在一般三角形中，遇到中点，常作中位线或构造“”字型全等三角形. 课时三级达标 A级 双基过手 1.如图,D,E,F分别为△ABC三边的中点.若△ABC的周长为10,则△DEF 的周长为 . 2.如图,在四边形ABCD中,AD∥BC,AD= BC,CD=BC,E,F分别是BD,CD的中点,连接AE,EF.若BC=2,则四边形 AEFD的周长为 . 3.如图,在 ABCD 中,对角线AC,BD相交于点O,E是边AB的中点.已知BC=10,则OE= . 4.(1)如图,EF 是△ABC的中位线,BD 平分∠ABC,交 EF于点 D.若BC=8,DF=1,则EB= . (2)如图,在Rt△ABC中,∠ACB=90°,D为线段AB的中点,延长BC 至点E,使 BC=CE,连接DE,F为DE 的中点,连接CF.若CD=6,则CF的长为 . 5.在△ABC中,D,E分别是△ABC的边AB,AC的中点,连接DE.若∠C=68°,则∠AED= ( ) A.22° B.68° C.96° D.112° 6.如图,在 Rt△ABC中,∠ACB=90°,∠B=30°,CM 是斜边AB 上的中线,E,F 分别为BM,BC的中点.若EF=1,则AB= ( ) A.3 B.3.5 C.4 D.4.5 7.如图,HF=AF,D,E,F 分别是三边的中点，则 DE 与FH 的大小关系是 ( ) A. DEFH C. DE=FH D. 不能确定 8.如图,在△ABC中,BD平分∠ABC,AF⊥BD于点 E,交 BC 于点 F,G 是 AC 的中点.若 BC=10,AB=7,则EG的长为 ( ) A.1.5 B.2 C.2.5 D.3.5 9.(1)四边形 ABCD是平行四边形,对角线AC,BD交于点O, E 是 AB 边上一点, 连接OE，求证： (2)如图,在等腰△ABC中,AB=AC=5,BC=6,D,E分别为AB,BC边上的中点,连接 DE 并延长到点 F,使得 EF =2ED,连接 AE,CF,求 CF的长. 10.(1)如图,在△ABC中,AB=12cm,AC=8cm,AD，AE分别是其角平分线和中线，过点 C 作CG⊥AD于点F,交AB于点G,连接EF,求线段EF的长. (2)如图,在 中， D,E分别为AC，BC的中点， ,过点 B 作. 交 DE 的延长线于点F，求四边形ABFD的面积. B级 能力提升 11.如图,在平行四边形ABCD中,E是CD 的中点,F 是AE 的中点,CF 交BE 于点G.若BE=3,则GE= . 12.如图,在平行四边形ABCD 中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点，有下列结论：①四边形 BEFG 是平行四边形;②BE⊥AC;③EG=FG;④EA平分∠GEF.其中正确结论的序号是 . 13.如图,在 Rt△ABC 中,∠ACB = 90°,∠BAC=30°,AC=8,BC=6,P是平面内一个动点,且AP=3,Q为BP 的中点,在 P 点运动过程中,设线段CQ的长度为m，则m的取值范围是 . 14.如图,点 E在平行四边形外,连接BE,DE,延长AC交DE 于点F,F 为DE 的中点. (1)求证: (2)若 求BE的长. C级 综合拓展 15.如图,在四边形 ABCD 中,E,F 分别是AD,BC的中点. (1)若 求EF的长; (2)若 求证： ... ...