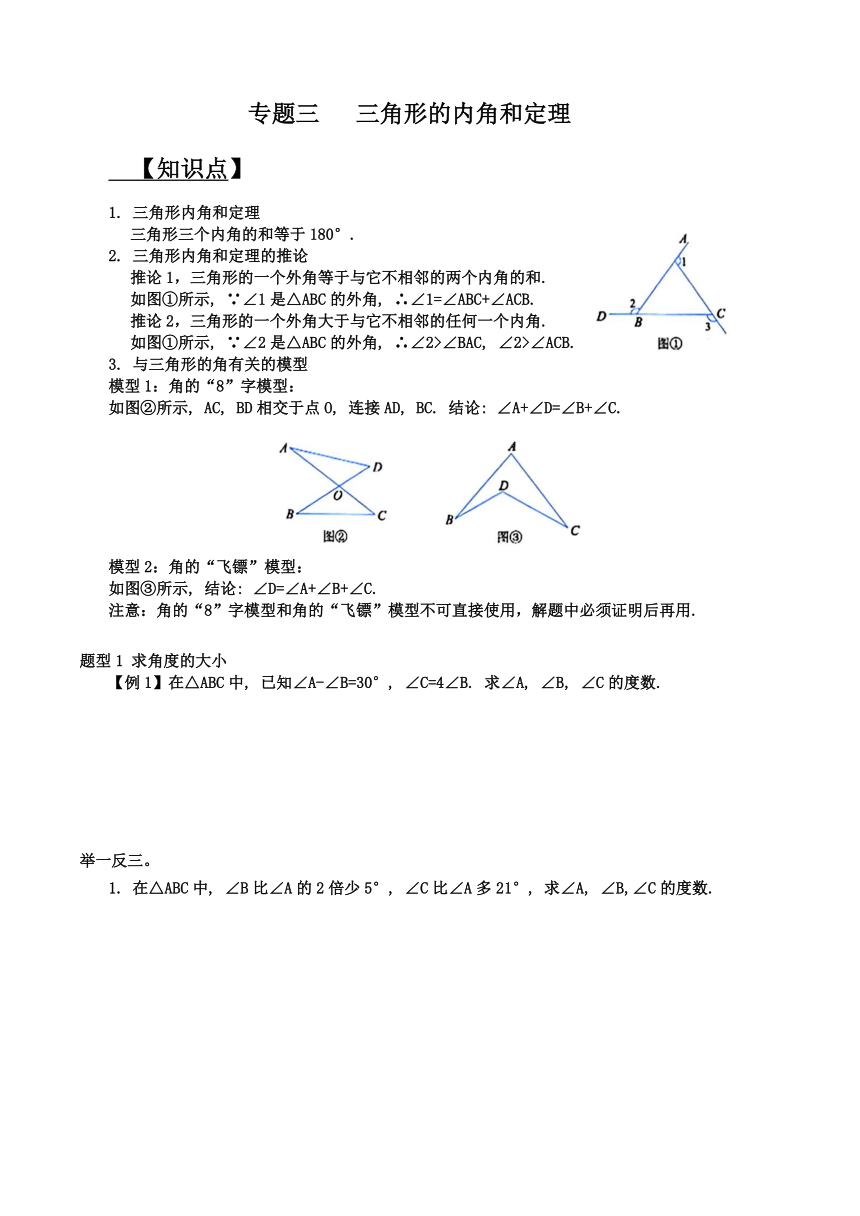
专题三 三角形的内角和定理 【知识点】 1. 三角形内角和定理 三角形三个内角的和等于180°. 2. 三角形内角和定理的推论 推论1,三角形的一个外角等于与它不相邻的两个内角的和. 如图①所示, ∵∠1是△ABC的外角, ∴∠1=∠ABC+∠ACB. 推论2,三角形的一个外角大于与它不相邻的任何一个内角. 如图①所示, ∵∠2是△ABC的外角, ∴∠2>∠BAC, ∠2>∠ACB. 3. 与三角形的角有关的模型 模型1:角的“8”字模型: 如图②所示, AC, BD相交于点O, 连接AD, BC. 结论: ∠A+∠D=∠B+∠C. 模型2:角的“飞镖”模型: 如图③所示, 结论: ∠D=∠A+∠B+∠C. 注意:角的“8”字模型和角的“飞镖”模型不可直接使用,解题中必须证明后再用. 题型1 求角度的大小 【例1】在△ABC中, 已知∠A-∠B=30°, ∠C=4∠B. 求∠A, ∠B, ∠C的度数. 举一反三。 1. 在△ABC中, ∠B比∠A的2倍少5°, ∠C比∠A多21°, 求∠A, ∠B,∠C的度数. 题型2 判断三角形的形状 【例2】在△ABC中, 已知 试判断这个三角形的形状. 举一反三。 2. 一个三角形的三个内角度数的比是3∶7∶10,最大的内角是多少度 这个是什么三角形 题型3 利用分类讨论思想求角度 【例3】已知非直角三角形ABC中, ,高BD和CE所在直线交于点H,求. 的度数. 举一反三。 3. 在 中, BD是AC边上的高, 求 的度数. 题型4 三角形的折叠与求角 【例4】生活中到处都存在着数学知识,只要同学们学会用数学的眼光观察生活,就会有许多意想不到的收获,如下两幅图都是由同一副三角板拼凑得到的: (1) 如图①所示, 求∠ABC的度数; (2) 如图②所示, 若AE∥BC, 则. 举一反三。 4.(1) 如图①所示,将直角三角形(∠ACB 为直角) 沿线段 CD折叠使点 B 落在点 B'处, 若 则 (2) 如图②所示, 纸片 中, 将纸片的一角沿ED折叠,使点 A 落在△ABC外点A'处, 求∠1-∠2的度数. 题型5 入射角与反射角的问题 【例5】光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ,Ⅱ之间来回反射,已知 求 的度数. 举一反三。 5. 光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ,Ⅱ之间来回反射,已知 ,求∠γ的度数. 191 题型6 应用三角形内角和定理的推论1求角的度数 【例6】如图所示, 中, ∠BAD=∠CBE=∠ACF, ∠FDE=64°, ∠DEF=43°, 求 各内角的度数. 举一反三。 6. 如图所示, △ABC的一条外角平分线是 CE, F是CA 延长线上一点, FG∥CE交AB于点G. 若∠DCE=50°, ∠B=40°, 求∠FGA的度数. 题型7 应用三角形内角和定理的推论2求证角或线段的不等关系 【例7】如图所示,已知在 中, A D平分∠BAC, 交BC于点 D. 求证: . 举一反三。 7. 如图所示,在 中, AD平分 于D, 求证: 考点8 三角形两内角平分线夹角 【例8】已知在 中, (1) 如图①所示, 的角平分线交于点O,求 的度数: (2) 如图②所示. 的三等分线交于点 则. (3) 如图③所示, 的n等分线交于点 则 (用含n的代数式) 举一反三。 8. 如图所示, 于D,试探究 与 之间的数量关系. 考点9 三角形两外角平分线夹角 【例9】如图, 点 P是 两条外角平分线的交点,求证: 举一反三· 9. 如图所示,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AC平分. BC平分∠ABy, 求∠C的度数. 考点10 三角形一内角平分线与一外角平分线的夹角 【例10】如图所示, 点 D 是BC延长线上一点, PB平分. PC平分 求证: 举一反三。 10. 如图所示, 试探究 之间的数量关系. 考点11 角平分线+高线夹角模型 【例11】(1)已知△ABC中, ∠B>∠C, AD⊥BC于点D, AE 平分∠BAC,如图①所示, 设∠B=x,∠C=y, 试用x, y表示∠DAE, 并说明理由; (2) 在图②中, 其他条件不变, 若把“AD⊥BC于点 D”改为“F是AE上一点, FD⊥BC于点 D”,试用x,y表示 (3) 在图③中,若把(2)中的“点F在AE上”改为“点F是A ... ...
~~ 您好,已阅读到文档的结尾了 ~~