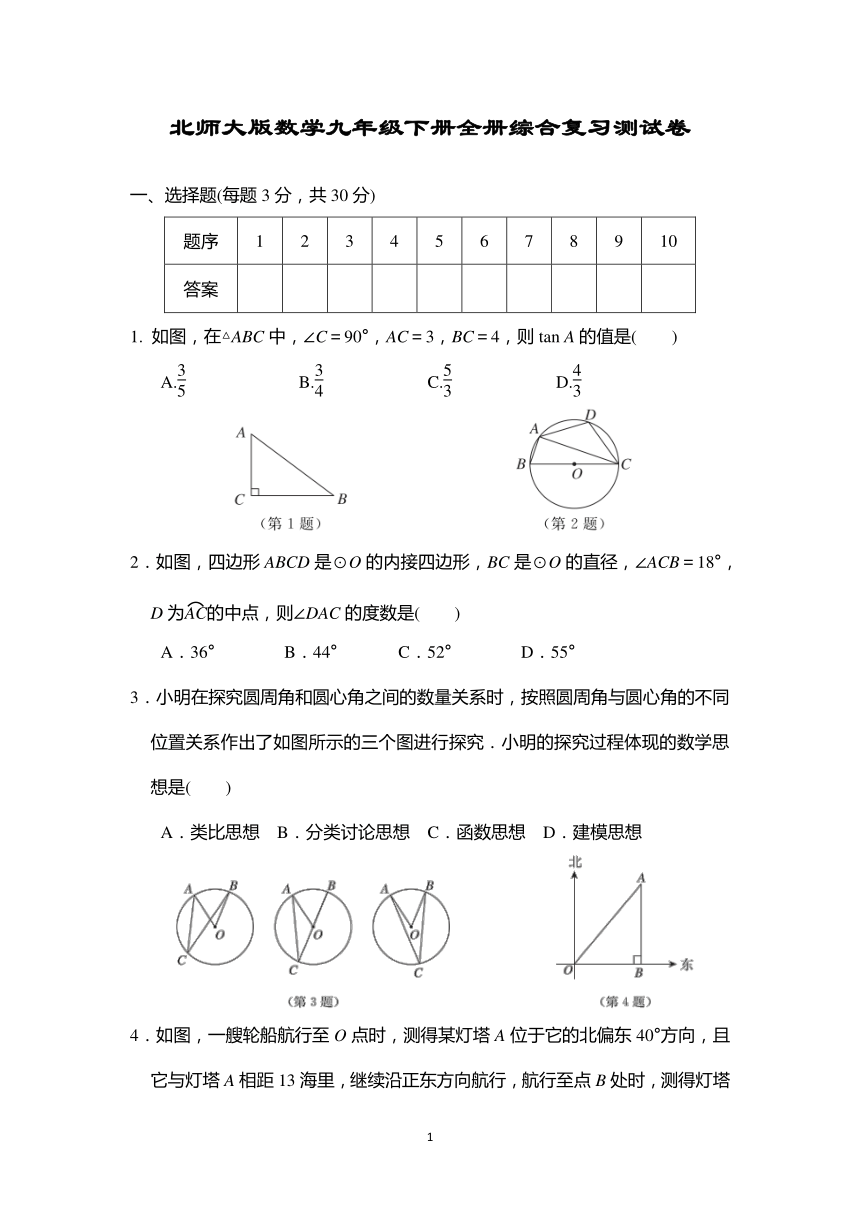
北师大版数学九年级下册全册综合复习测试卷（含答案）

北师大版数学九年级下册全册综合复习测试卷 一、选择题(每题3分，共30分) 题序 1 2 3 4 5 6 7 8 9 10 答案 1. 如图，在△ABC中，∠C＝90°，AC＝3，BC＝4，则tan A的值是(　　) A. B. C. D. 2．如图，四边形ABCD是⊙O的内接四边形，BC是⊙O的直径，∠ACB＝18°，D为的中点，则∠DAC的度数是(　　) A．36° B．44° C．52° D．55° 3．小明在探究圆周角和圆心角之间的数量关系时，按照圆周角与圆心角的不同位置关系作出了如图所示的三个图进行探究．小明的探究过程体现的数学思想是(　　) A．类比思想 B．分类讨论思想 C．函数思想 D．建模思想 4．如图，一艘轮船航行至O点时，测得某灯塔A位于它的北偏东40°方向，且它与灯塔A相距13海里，继续沿正东方向航行，航行至点B处时，测得灯塔A恰好在它的正北方向，则AB的距离可表示为(　　) A．13cos 40°海里 B．13sin 40°海里 C.海里 D.海里 5．将二次函数y＝x2＋6x－1化为y＝a(x－h)2＋k的形式为(　　) A．y＝(x－3)2－8 B．y＝(x＋3)2－8 C．y＝(x－3)2－10 D．y＝(x＋3)2－10 6．将抛物线y＝x2－2x＋3向上平移2个单位长度，再向左平移3个单位长度后，得到的抛物线的表达式为(　　) A．y＝(x＋2)2＋4 B．y＝(x－4)2＋4 C．y＝(x＋2)2 D．y＝(x－4)2＋6 7．已知⊙O内有一点P，过点P的所有弦中，最长的为10，最短的为8，则OP的长为(　　) A．6 B．5 C．4 D．3 8．如图，⊙A过O，D，C，B四点，连接CO，CD，若∠DCO＝30°，点B的坐标为(4，0)，则点D的坐标为(　　) A．(0，2) B. C. D．(0，3) 9.如图，在正方形网格中，每个小正方形的边长都为1，点A，B，C，D，O都在格点(小正方形的顶点)上，若和所在圆的圆心均为点O，则阴影部分的面积为(　　) A．2π－2 B．π－2 C．2π D．π 10．如图是二次函数y＝ax2＋bx＋c图象的一部分，其对称轴是直线x＝－1，且过点(－3，0)，下列结论：①abc<0；②2a－b＝0；③方程ax2＋bx＋c－1＝0有两个相等的实数根；④a＋c<0；⑤若(－2，y1)，是图象上的两点，则y1>y2.其中正确的是(　　) A．①②④ B．②③④ C．③④⑤ D．①③⑤ 二、填空题(每小题3分，共15分) 11. 抛物线y＝2x2－4x＋3的对称轴是_____． 12．如图，P是⊙O外一点，过P引⊙O的切线PA，PB，若∠APB＝48°，则∠AOB＝_____°. 13．如图，折扇的骨柄长为27 cm，折扇张开的角度为120°，图中的长为_____cm(结果保留π)． 14．如图，△ABC内接于⊙O，连接OA，OB.若∠OAB＝65°，则∠ACB的度数为_____． 15.太原地铁2号线是山西省第一条开通运营的地铁线路，如图是该地铁某站扶梯的示意图，扶梯AB的坡度i＝5∶12(i为铅直高度与水平宽度的比)．王老师乘扶梯从扶梯底端A以0.5米/秒的速度用40秒到达扶梯顶端B，则王老师上升的铅直高度BC为_____米． 三、解答题(本大题共8个小题，共75分) 16．(5分)计算： (1)|－3|＋·tan 30°－－(2 025－π)0；　　　(2)tan2 60°－2sin 30°－2cos 45°. 17．(8分)如图，在△ABC中，CD⊥AB于点D，∠ACD＝45°，∠DCB＝60°，CD＝40，求AB的长． 18．(8分)项目化学习：某校“项目化学习”小组的同学把“测量风力发电叶片长度”作为一项课题活动，利用课余时间完成了实践调查，并制作了如下活动报告． 项目 测量风力发电叶片长度 调查方式 资料查阅、电力部门走访、实地查看了解 调查内容 目的 测量风力发电叶片长度 材料 测角仪，皮尺等 风车安装示意图 相关数据及说明：小明首先通过C处的铭牌简介得知风车杆BC的高度为95 m，然后沿水平方向走到D处，再沿着斜坡DE走了25 m到达E处观察风叶，风叶AB在如图所示的铅垂方向，测得点A的仰角为68°，风叶A′B在如图所示的水平方向，测得点A′的仰角为45°，斜坡DE的坡度i＝1∶0.75，小明身高忽略不计 计算结果 ... ...