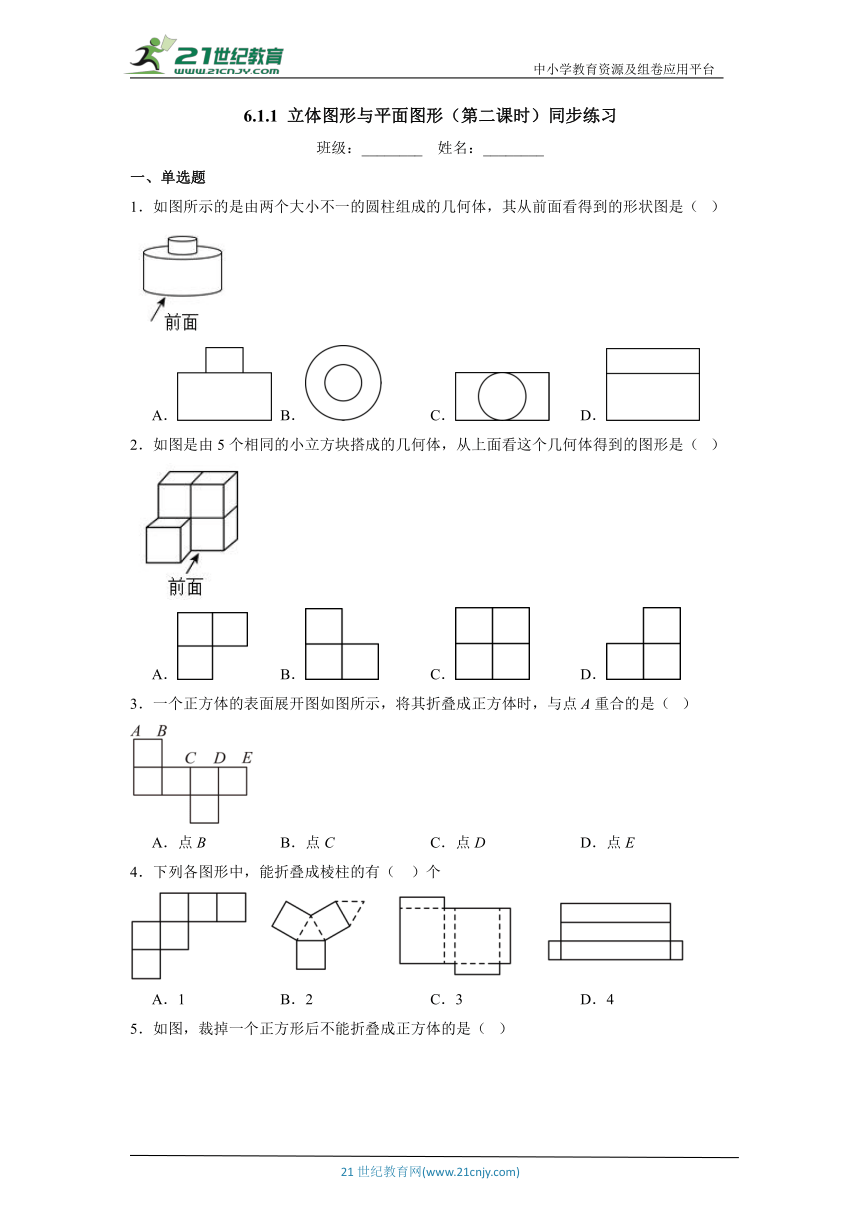
中小学教育资源及组卷应用平台 6.1.1 立体图形与平面图形(第二课时)同步练习 班级:_____ 姓名:_____ 一、单选题 1.如图所示的是由两个大小不一的圆柱组成的几何体,其从前面看得到的形状图是( ) A. B. C. D. 2.如图是由5个相同的小立方块搭成的几何体,从上面看这个几何体得到的图形是( ) A. B. C. D. 3.一个正方体的表面展开图如图所示,将其折叠成正方体时,与点A重合的是( ) A.点B B.点C C.点D D.点E 4.下列各图形中,能折叠成棱柱的有( )个 A.1 B.2 C.3 D.4 5.如图,裁掉一个正方形后不能折叠成正方体的是( ) A.① B.② C.③ D.④ 二、填空题 6.如图,是一个几何体表面的展开图,则这个几何体是 . 7.下面的图形经过折叠可以围成的几何体名称是 . 8.如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体从三个方向看到的形状图没有发生变化的是从 看到的形状图. 9.如图,这是由若干个小立方体搭起来的几何体的正面、侧面所看到的图,那么这个几何体至少应该由 个小立方体组成. 10.一个长方体的展开图如图所示,每个面分别标上的了六个数字(数字在长方体的内侧),已知3、5、6三面面积之和是,且5号面是一个边长3厘米的正方形.这个长方体的体积是 . 三、解答题 11.在平整的地面上,有若干个完全相同的棱长为的小正方体堆成一个几何体,如图所示,请画出这个几何体从三个方向看到的图形. 12.小雅同学在学习了立体图形的展开与折叠后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: (1)小明总共剪开了_____条棱. (2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全. (3)小明说:已知这个长方体纸盒高为,底面是一个正方形,并且这个长方体纸盒所有棱长的和是,求这个长方体纸盒的体积. 答案与解析 一、单选题 1.如图所示的是由两个大小不一的圆柱组成的几何体,其从前面看得到的形状图是( ) A. B. C. D. 【答案】A 【解析】本题考查了从不同方向看几何体,运用空间想象能力观察是关键. 根据从前面看到的图形求解即可. 解:从前面看得到的形状图是. 故选:A. 2.如图是由5个相同的小立方块搭成的几何体,从上面看这个几何体得到的图形是( ) A. B. C. D. 【答案】A 【解析】本题主要考查从不同方向看简单组合体,从上面看这个几何体有两行,从上到下小正方形个数分别为2和1. 解:由题意知,该几何体从上面看得到的图形是: 故选:A. 3.一个正方体的表面展开图如图所示,将其折叠成正方体时,与点A重合的是( ) A.点B B.点C C.点D D.点E 【答案】C 【解析】本题考查展开图折叠成几何体,根据正方体表面展开图的特征进行解答即可;掌握正方体表面展开图的特征是正确判断的关键. 解:如图,将这个正方体的表面展开图折成一个正方体,点A与点D重合, 故选:C. 4.下列各图形中,能折叠成棱柱的有( )个 A.1 B.2 C.3 D.4 【答案】B 【解析】本题考查了展开图折叠成几何体,利用展开图的形状是解题关键,注意几何体的上底面与下底面相对. 根据棱柱展开图的形状,可得答案. 解:第一个图无法可折叠成棱柱;第二图可折叠成三棱柱;第三个图可折叠成长方体,即四棱柱;第四个图无法折叠成棱柱;所以能折叠成棱柱的有2个. 故选:B 5.如图,裁掉一个正方形后不能折叠成正方体的是( ) A.① B.② C.③ D.④ 【答案】A 【解析】本题主要考查正方体的展开 ... ...
~~ 您好,已阅读到文档的结尾了 ~~