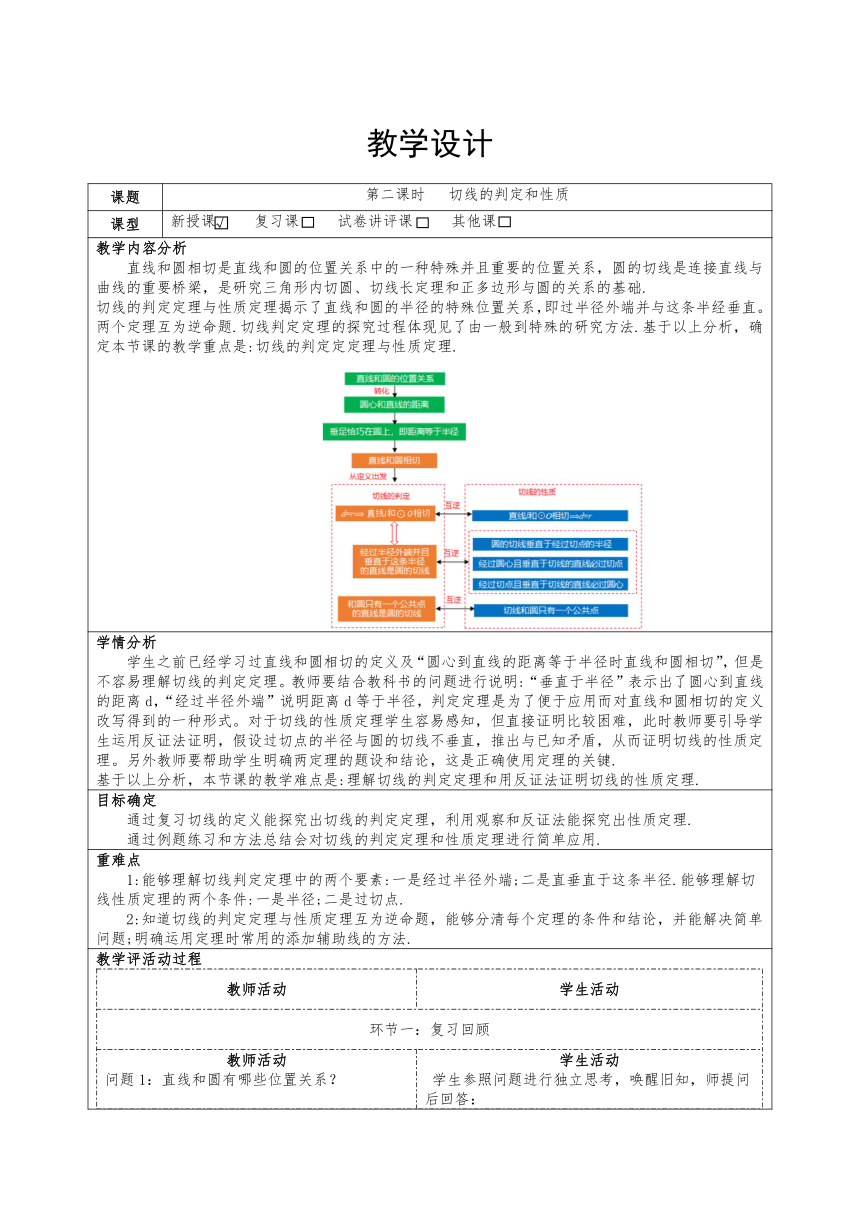
教学设计 课题 ( √ )第二课时 切线的判定和性质 课型 新授课 复习课 试卷讲评课 其他课 教学内容分析 直线和圆相切是直线和圆的位置关系中的一种特殊并且重要的位置关系,圆的切线是连接直线与曲线的重要桥梁,是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础. 切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系,即过半径外端并与这条半经垂直。两个定理互为逆命题.切线判定定理的探究过程体现见了由一般到特殊的研究方法.基于以上分析,确定本节课的教学重点是:切线的判定定定理与性质定理. 学情分析 学生之前已经学习过直线和圆相切的定义及“圆心到直线的距离等于半径时直线和圆相切”,但是不容易理解切线的判定定理。教师要结合教科书的问题进行说明:“垂直于半径”表示出了圆心到直线的距离d,“经过半径外端”说明距离d等于半径,判定定理是为了便于应用而对直线和圆相切的定义改写得到的一种形式。对于切线的性质定理学生容易感知,但直接证明比较困难,此时教师要引导学生运用反证法证明,假设过切点的半径与圆的切线不垂直,推出与已知矛盾,从而证明切线的性质定理。另外教师要帮助学生明确两定理的题设和结论,这是正确使用定理的关键. 基于以上分析,本节课的教学难点是:理解切线的判定定理和用反证法证明切线的性质定理. 目标确定 通过复习切线的定义能探究出切线的判定定理,利用观察和反证法能探究出性质定理. 通过例题练习和方法总结会对切线的判定定理和性质定理进行简单应用. 重难点 1:能够理解切线判定定理中的两个要素:一是经过半径外端;二是直垂直于这条半径.能够理解切线性质定理的两个条件:一是半径;二是过切点. 2:知道切线的判定定理与性质定理互为逆命题,能够分清每个定理的条件和结论,并能解决简单问题;明确运用定理时常用的添加辅助线的方法. 教学评活动过程 教师活动学生活动环节一:复习回顾教师活动 问题1:直线和圆有哪些位置关系? 追问:目前你都会用哪些方法判断直线和圆相切?学生活动 学生参照问题进行独立思考,唤醒旧知,师提问后回答: 直线和圆的位置关系有:相交、相切、相离 根据直线和圆只有一个公共点、 d=r(d为圆心到直线的距离,r为圆半径)判断直线和圆相切. 学生回答追问问题,总结判断方法: 方法1:直线与圆有唯一公共点 方法2:圆心到直线的距离等于半径设计意图通过问题的形式唤起学生旧知,通过追问引发学生反思,为本节课学习切线的判定定理和性质定理作好铺垫,促使学生构建起知识间的相互联系。环节二:探究新知一教师活动 师提出问题,引发学生思考: 问题2:如图 ,在⊙O中,经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l的距离是多少?直线l 和⊙O有什么位置关系? 追问1:直线l满足什么条件时圆心O到直线l的距离才会等于半径? 切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 若学生对判定定理内容不理解,教师可进行说明:“垂直于半径”表示出了圆心到直线的距离d,“经过半径外端”说明距离d等于半径r.判定定理是为了便于应用直线和圆相切的定义而改写的一种形式. 追问2:如果说切线的定义是分别从直线和圆的公共点个数和“ d=r”这两种数量关系的角度得出了直线和圆相切的位置关系,那么判定定理又是从哪个角度得出了直线和圆相切的位置关系呢?学生活动 学生独立思考后回答: 圆心0到直线l的距离是OA,也就是O的半径,利用数量关系d=r,判断出直线l是⊙O的切线. 通过教师的追问引发学生再次思考,从而得到切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 追问2的问题有难度,学生独立思考后再小组交流思维碰撞,学生代表回答: 圆心与直线的位置关系 圆与直线的位置关系设计意图通过问 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

