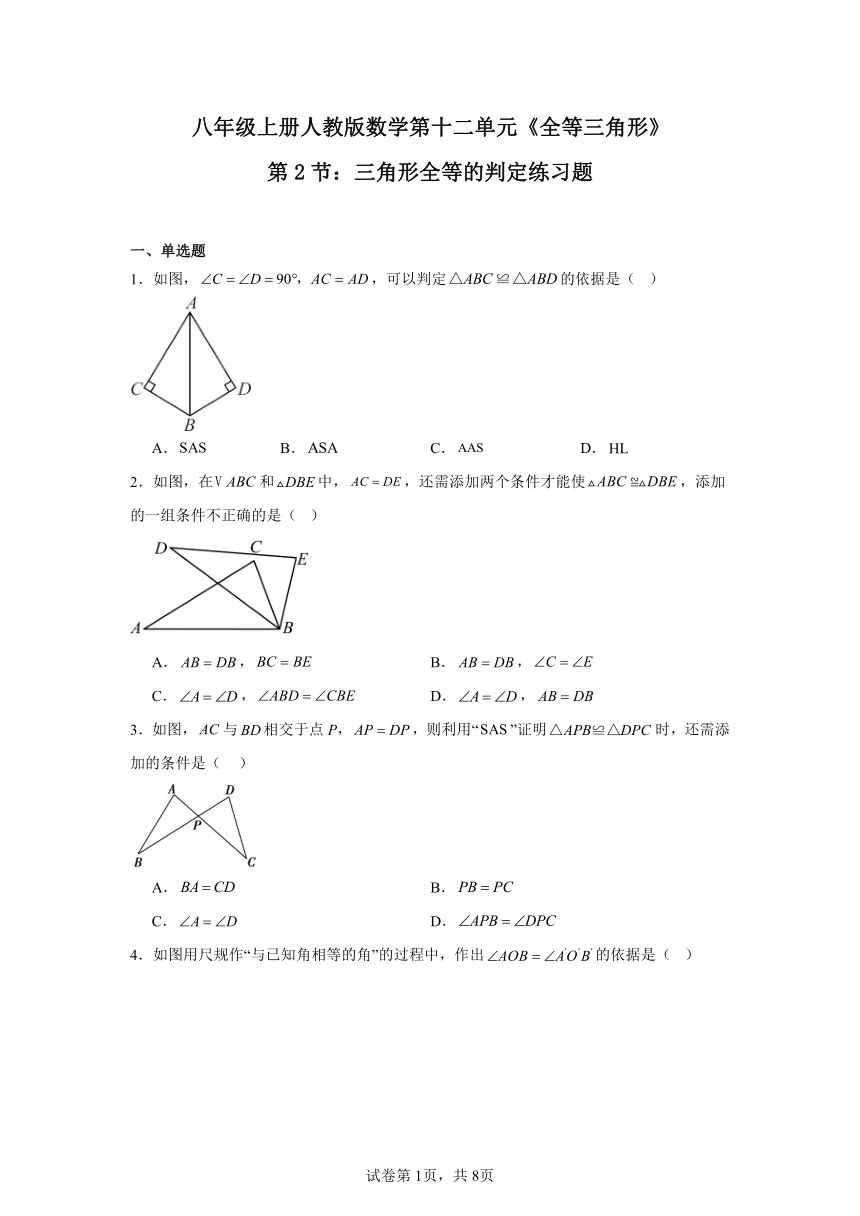
八年级上册人教版数学 12.2 三角形全等的判定 练习题（含答案）

八年级上册人教版数学第十二单元《全等三角形》 第2节：三角形全等的判定练习题 一、单选题 1．如图，，可以判定的依据是（ ） A． B． C． D． 2．如图，在和中，，还需添加两个条件才能使，添加的一组条件不正确的是（ ） A．， B．， C．， D．， 3．如图，与相交于点P，，则利用“”证明时，还需添加的条件是（ ） A． B． C． D． 4．如图用尺规作“与已知角相等的角”的过程中，作出的依据是（ ） A． B． C． D． 5．如图，D为等腰三角形内一点，，，，，则的度数为（ ） A． B． C． D． 6．如图，，添加一个条件，可使用“”判定与全等，以下给出的条件适合的是（ ） A． B． C． D． 7．中，是边的中线，且的长度为奇数，，则等于（ ） A．1 B．3 C．5 D．7 8．如图，在中，，，，将绕点B按顺时针方向旋转得到，过点C作，垂足为点F，当时，BF的长为（ ） A． B． C． D． 9．如图，，，于点E，于点D，，，则的长是（ ） A．8 B．4 C．3 D．2 10．如图，已知AC平分，于E，，则下列结论①；②；③；④．其中，正确结论的个数（ ） A．1个 B．2个 C．3个 D．4个 二、填空题 11．如图，点是，的中点，要用“”证明，则只需添加一个适当的条件是 ． 12．如图，与相交于点F，与相交于点G，若，则 ． 13．如图，，，将绕D逆时针旋转90°至，连接AE，若，则的面积是 ． 14．如图，某同学不小心把一块三角形玻璃碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带 块（填“”、“ ”或“” ． 15．如图，，，，，点P和点Q同时从点A出发，分别在线段和射线上运动，且，当 时，以点A，P，Q为顶点的三角形与全等． 16．在中，是中线，已知，则中线的取值范围是 ． 17．如图，在中，，过点作，且，连接，若，则的长为 ． 18．在学习完“探索三角形全等的条件”一节后，一同学总结出很多全等三角形的模型，他设计了以下问题给同桌解决：如图，做一个“U”字形框架，其中，、足够长，于A，于B，点M从B出发向A运动，同时点N从B出发向Q运动，使M、N运动的速度之比，当两点运动到某一瞬间同时停止，此时在射线上取点C，使与全等，则线段AC的长为 ． 三、解答题 19．如图，在中，点在边的延长线上，过点作，点是射线上一个点，满足． (1)使用尺规在射线的左侧作，与射线交于点．（不写作法，保留作图痕迹） (2)求证：． 20．如图，点、、、在同一直线上，，，． 求证：． 21．已知：如图，与，，，是的中线，是的中线，且．求证：． 22．如图，在中，于点E，于点D．求证： (1)； (2) 23．如图，，，，． (1)求证：； (2)若，，求的长． 24．在通过构造全等三角形解决问题的过程中，有一种方法叫做倍长中线法． (1)如图（1），是的中线．且．延长至点．使．连接．求证：． (2)如图（2），是的中线，点在的延长线上，，，求证：． 25．如图，在平面直角坐标系中，为原点，点在轴正半轴上，点，点在第二象限，，． (1)求的值； (2)当时． ①求三角形的面积； ②在坐标平面内是否存在点（不与点重合），使与全等？若存在，求出所有点的坐标；若不存在，请说明理由． 试卷第1页，共3页 试卷第1页，共3页 参考答案： 题号 1 2 3 4 5 6 7 8 9 10 答案 D B B D D D B D C D 11． 12． 13．3 14． 15．10或20 16． 17．3 18．或 19．（1）解：如图，即为所求作的角 （2）证明：， ， 在和中， ， ， ， ． 20．证明：， ， ， ，即， 在和中， ， ， ． 21．证明：∵是的中线，是的中线， ∴，， 又∵， ∴， 在和中，， ∴， ∴， 在和中，， ∴． 22．（1）证明∶∵， ∴， ∴， ∴， 又∵， ∴． 在与中， ， ∴．． （2）解：∵， ∴， ∴，即． 23．（1），， 且，， 在与， ， ． （2）， ，， ． 24．（1）证明：是 ... ...