5.7 三角函数的应用（单元教学设计）

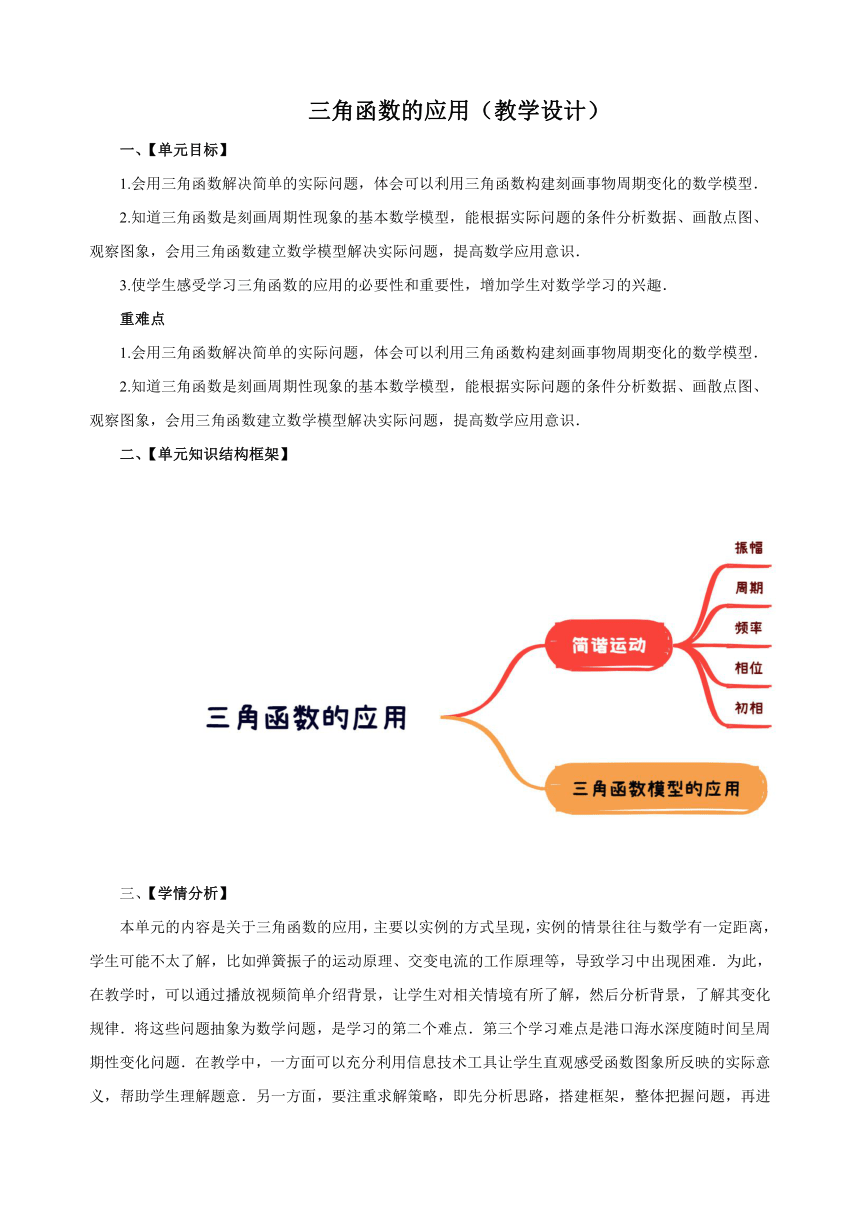
三角函数的应用（教学设计） 一、【单元目标】 1.会用三角函数解决简单的实际问题，体会可以利用三角函数构建刻画事物周期变化的数学模型． 2.知道三角函数是刻画周期性现象的基本数学模型，能根据实际问题的条件分析数据、画散点图、观察图象，会用三角函数建立数学模型解决实际问题，提高数学应用意识． 3.使学生感受学习三角函数的应用的必要性和重要性，增加学生对数学学习的兴趣． 重难点 1.会用三角函数解决简单的实际问题，体会可以利用三角函数构建刻画事物周期变化的数学模型． 2.知道三角函数是刻画周期性现象的基本数学模型，能根据实际问题的条件分析数据、画散点图、观察图象，会用三角函数建立数学模型解决实际问题，提高数学应用意识． 二、【单元知识结构框架】 三、【学情分析】 本单元的内容是关于三角函数的应用，主要以实例的方式呈现，实例的情景往往与数学有一定距离，学生可能不太了解，比如弹簧振子的运动原理、交变电流的工作原理等，导致学习中出现困难．为此，在教学时，可以通过播放视频简单介绍背景，让学生对相关情境有所了解，然后分析背景，了解其变化规律．将这些问题抽象为数学问题，是学习的第二个难点．第三个学习难点是港口海水深度随时间呈周期性变化问题．在教学中，一方面可以充分利用信息技术工具让学生直观感受函数图象所反映的实际意义，帮助学生理解题意．另一方面，要注重求解策略，即先分析思路，搭建框架，整体把握问题，再进是求解细节． 四、【教学设计思路/过程】 课时安排：约1课时 教学重点：用三角函数模型解决一些具有周期变化规律的实际问题． 教学难点：将某些实际问题抽象为三角函数模型． 教学方法/过程： 五、【教学问题诊断分析】 环节一、情景引入，温故知新 情景1：前面我们学习了三角函数图象和性质，了解到三角函数是刻画现实世界中周期性现象的理想模型．今天这节课开始，我们研究三角函数的应用．对于某些实际问题，三角函数是比较理想化的模型；而对于有些实际问题，三角函数却只能是在一定范围内近似地刻画它的变化规律的模型． 问题1：你能举出物理或生活中具有周期性现象的实例吗 【破解方法】学生经过思考和讨论之后，举出一些物理或生活中的实例，教师引导学生进行补充、梳理，再过渡到今天要解决的两个实例． 周期性现象的例子包括以下几方面： （1）匀速圆周运动，如表的指针的转动、筒车旋转、摩天轮旋转等． （2）物理学中的周期性现象，如钟摆、弹簧振子运动、发电机产生的交变电流等． 环节二、抽象概念，内涵辨析 问题2：某个弹簧振子（简称振子）在完成一次全振动的过程中，时间t（单位：s）与位移y（单位：mm）之间的对应数据如表所示．试根据这些数据确定这个振子的位移关于时间的函数解析式． 请你查阅资料，了解振子的运动原理． 振子的振动具有循环往复的特点，由振子振动的物理学原理可知，其位移狔随时间狋的变化规律可以用函数y=Asin（ωt+φ ）来刻画．根据已知数据作出散点图，如图所示． 【破解方法】由数据表和散点图可知，振子振动时位移的最大值为，因此；振子振动的周期为，即，解得；再由初始状态振子的位移为，可得，因此．所以振子位移关于时间的函数解析式为，． 【归纳新知】函数中，，，的物理意义 1、简谐运动的振幅就是． 2、简谐运动的周期． 3、简谐运动的频率． 4、称为相位． 5、时的相位称为初相． 问题3：如图（1）所示的是某次实验测得的交变电流（单位：A）随时间沶（单位：S）变化的图象．将测得的图象放大，得到图（2） （1）求电流i随时间t变化的函数解析式； （2）当时，求电流． 请你查阅资料，了解交变电流的产生原理． 【破解方法】由交变电流的产生原理可知，电流随时间的变化规律可用来刻画，其中 ... ...